Diketahui:
\(\textbf{L}_1 : \text{lingkaran besar}\)
\(\textbf{P}_1 : \text{pusat lingkaran 1}\)
\(\textbf{R} : \text{jari-jari lingkaran 1}\)
\(\textbf{L}_2 : \text{lingkaran kecil}\)
\(\textbf{P}_2 : \text{pusat lingkaran 2}\)
\(\textbf{r} : \text{jari-jari lingkaran 2}\)
\(\textbf{P}_1\textbf{P}_2 : \text{jarak antara kedua pusat lingkaran}\)
A. Konsentris (sepusat)
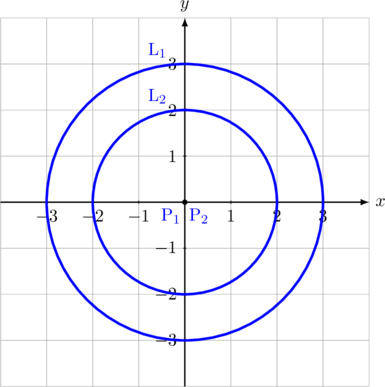
\(\text{L}_1\) konsentris dengan \(\text{L}_2\), artinya \(\text{L}_1\) dan \(\text{L}_2\) memiliki titik pusat yang sama.
B. Bersinggungan di dalam
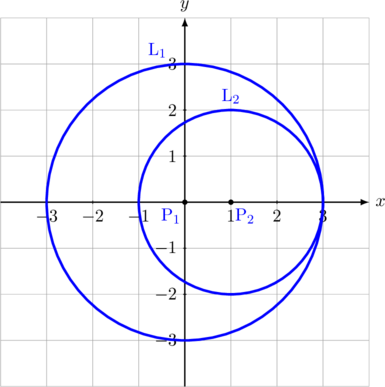
\(\text{L}_2\) berada di dalam lingkaran \(\text{L}_1\) dan bersinggungan.
\(\color{blue}\textbf{P}_1\textbf{P}_2 = \textbf{R}\:-\:\textbf{r}\)
C. Berpotongan
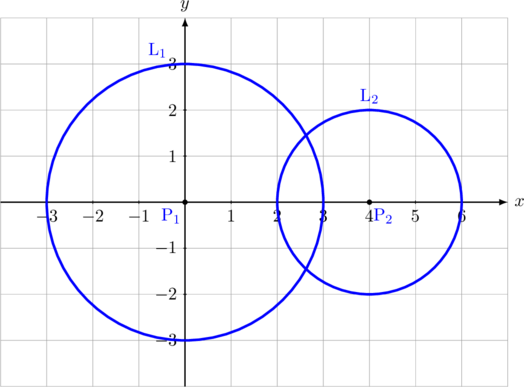
\(\text{L}_1\) berpotongan dengan \(\text{L}_2\)
\(\color{blue}\textbf{R} \:-\: \textbf{r} < \textbf{P}_1\textbf{P}_2 < \textbf{R} + \textbf{r}\)
D. Bersinggungan di luar
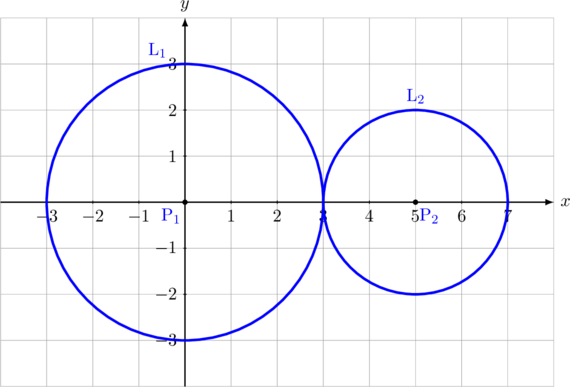
\(\text{L}_1\) bersinggungan di luar dengan \(\text{L}_2\)
\(\color{blue}\textbf{P}_1\textbf{P}_2 = \textbf{R} + \textbf{r}\)
E. Saling lepas
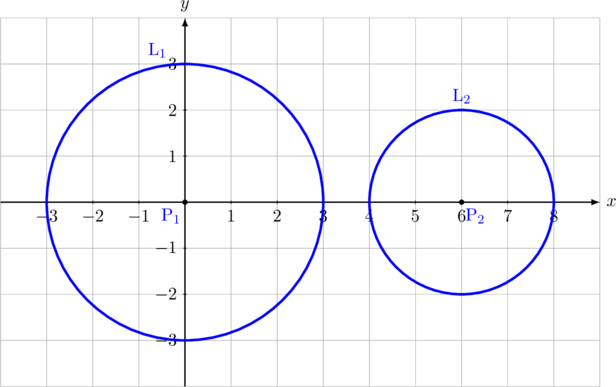
\(\text{L}_1\) terpisah dengan \(\text{L}_2\)
\(\color{blue}\textbf{P}_1\textbf{P}_2 > \textbf{R} + \textbf{r}\)
F. \(\textbf{L}_2\) berada di dalam \(\textbf{L}_1\) dan tidak sepusat maupun bersinggungan dalam
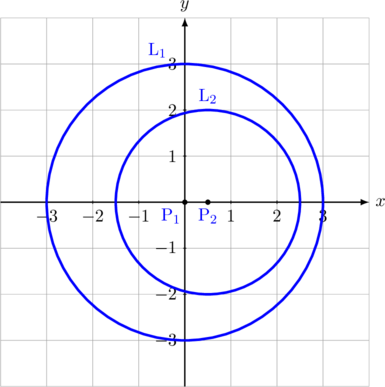
\(\text{L}_2\) berada di dalam \(\text{L}_1\), tidak sepusat maupun bersinggungan dalam
\(\color{blue}\textbf{P}_1\textbf{P}_2 < \textbf{R} \:-\: \textbf{r}\)
CONTOH SOAL
Soal 1
Selidikilah hubungan antara 2 lingkaran berikut:
\(\textbf{L}_1 : x^2 + y^2\:-\:4x\:-\:6y \:-\:51 = 0\)
\(\textbf{L}_2 : x^2 + y^2 \:-\:6x \:-\:2y + 1 = 0\)
Langkah 1: menentukan pusat dan jari-jari masing-masing lingkaran
\(\textbf{L}_1 : x^2 + y^2\:-\:4x\:-\:6y \:-\:51 = 0\)
\(\textbf{P}_1 = (-\frac{1}{2}(-4), -\frac{1}{2}(-6)) = (2, 3)\)
\(\textbf{R} = \sqrt{2^2 + 3^2\:-\:(-51)} = \sqrt{64} = 8\)
\(\textbf{L}_2 : x^2 + y^2 \:-\:6x \:-\:2y + 1 = 0\)
\(\textbf{P}_2 = (-\frac{1}{2}(-6), -\frac{1}{2}(-2)) = (3, 1)\)
\(\textbf{r} = \sqrt{3^2 + 1^2\:-\:1} = \sqrt{9} = 3\)
Langkah 2: menentukan jarak antara kedua pusat lingkaran
\(\textbf{P}_1 = (2, 3)\)
\(\textbf{P}_2 = (3, 1)\)
\(\textbf{P}_1\textbf{P}_2 = \sqrt{(x_2\:-\:x_1)^2 + (y_2\:-\:y_1)^2}\)
\(\textbf{P}_1\textbf{P}_2 = \sqrt{(3\:-\:2)^2 + (1\:-\:3)^2}\)
\(\textbf{P}_1\textbf{P}_2 = \sqrt{1^2 + (-2)^2}\)
\(\textbf{P}_1\textbf{P}_2 = \sqrt{5}\)
Langkah 3: menentukan hubungan antara kedua lingkaran
\(\textbf{P}_1\textbf{P}_2 < \textbf{R}\:-\:\textbf{r}\)
\(\sqrt{5} < 8\:-\:3\)
Karena jarak antara kedua pusat lingkaran kurang dari selisih jari-jari kedua lingkaran maka \(\text{L}_2\) berada di dalam \(\text{L}_1\), tidak sepusat dan tidak bersinggungan dalam.
Soal 2
Selidikilah hubungan antara 2 lingkaran berikut:
\(\textbf{L}_1 : x^2 + y^2\:-\:8x + 4y \:-\:16 = 0\)
\(\textbf{L}_2 : x^2 + y^2 + 16x \:-\:6y \:-\:27= 0\)
\(\textbf{L}_1 : x^2 + y^2\:-\:8x + 4y \:-\:16 = 0\)
Pusat lingkaran pertama:
\(\text{P}_1 = (4, -2)\)
Jari-jari lingkaran pertama:
\(\text{r}_1 = \sqrt{4^2 + (-2)^2\:-\:(-16)}\)
\(\text{r}_1 = \sqrt{16 +4 + 16}\)
\(\text{r}_1 = 6\)
\(\textbf{L}_2 : x^2 + y^2 + 16x \:-\:6y \:-\:27= 0\)
Pusat lingkaran kedua:
\(\text{P}_2 = (-8, 3)\)
Jari-jari lingkaran kedua:
\(\text{r}_2= \sqrt{(-8)^2 + 3^2\:-\:(-27)}\)
\(\text{r}_2 = \sqrt{64 + 9 + 27}\)
\(\text{r}_2 = 10\)
Menghitung jarak kedua pusat lingkaran:
\(\text{P}_1\cdot \text{P}_2 = \sqrt{(x_2 \:-\:x_1)^2 + (y_2 \:-\:y_1)^2}\)
\(\text{P}_1\cdot \text{P}_2 = \sqrt{(-8 \:-\:4)^2 + (3 \:-\:(-2))^2}\)
\(\text{P}_1\cdot \text{P}_2 = \sqrt{144 + 25}\)
\(\text{P}_1\cdot \text{P}_2 = 13\)
Karena \(r_2 \:-\:r_1 < \text{P}_1\cdot \text{P}_2 < r_1 + r_2\) yaitu \(10\:-\:6 < 13 < 6 + 10\) maka kedua lingkaran berpotongan.
Soal 3
Diketahui dua buah lingkaran
\(\textbf{L}_1 : x^2 + y^2\:-\:6x + 14y + 26 = 0\)
\(\textbf{L}_2 : x^2 + y^2 + 8x + 12y + m = 0\)
Jika kedua lingkaran bersinggungan dalam, maka tentukan nilai \(m\) yang memenuhi.
\(\textbf{L}_1 : x^2 + y^2\:-\:6x + 14y + 26 = 0\)
Pusat lingkaran pertama:
\(\text{P}_1 = (3, -7)\)
Jari-jari lingkaran pertama:
\(\text{r}_1 = \sqrt{3^2 + (-7)^2\:-\:26}\)
\(\text{r}_1 = \sqrt{9 +49 \:-\: 26}\)
\(\text{r}_1 = \sqrt{32} = 4\sqrt{2}\)
\(\textbf{L}_2 : x^2 + y^2 + 8x + 12y + m = 0\)
Pusat lingkaran kedua:
\(\text{P}_2 = (-4, -6)\)
Jari-jari lingkaran kedua:
\(\text{r}_2= \sqrt{(-4)^2 + (-6)^2\:-\:m}\)
\(\text{r}_2 = \sqrt{16 + 36 \:-\:m}\)
\(\text{r}_2 = \sqrt{52\:-\:m}\)
Menghitung jarak kedua pusat lingkaran:
\(\text{P}_1\cdot \text{P}_2 = \sqrt{(x_2 \:-\:x_1)^2 + (y_2 \:-\:y_1)^2}\)
\(\text{P}_1\cdot \text{P}_2 = \sqrt{(-4\:-\:3)^2 + (-6 + 7)^2}\)
\(\text{P}_1\cdot \text{P}_2 = \sqrt{49 + 1}\)
\(\text{P}_1\cdot \text{P}_2 = \sqrt{50} = 5\sqrt{2}\)
Kedua lingkaran saling bersinggungan dalam, maka \(\text{P}_1\cdot \text{P}_2 = \text{r}_2 \:-\: \text{r}_1\)
\(5\sqrt{2} = \sqrt{52\:-\:m} \:-\:4\sqrt{2}\)
\(9\sqrt{2} = \sqrt{52\:-\:m}\)
Kuadratkan kedua ruas,
\(162 = 52\:-\:m\)
\(m = 52\:-\:162\)
\(m = -110\)
