Kedudukan titik \((x_1, y_1)\) terhadap lingkaran apakah berada di dalam lingkaran, terletak pada lingkaran, atau di luar lingkaran dapat diketahui dengan menghitung nilai kuasa \((\textbf{K})\) titik tersebut terhadap lingkaran.
\(\color{blue}\textbf{K} = x^2_1 + y^2_2 \:-\:r^2\)
atau
\(\color{blue}\textbf{K} = (x_1\:-\:a)^2 + (x_2\:-\:b)^2 \:-\:r^2\)
atau
\(\color{blue}\textbf{K} = x^2_1 + y^2_1 + \text{A}x_1 + \text{B}y_1 + \text{C}\)
Jika \(\textbf{K} > 0\) maka titik berada di luar lingkaran
Jika \(\textbf{K} = 0\) maka titik terletak pada lingkaran
Jika \(\textbf{K} < 0\) maka titik terletak di dalam lingkaran
CONTOH SOAL
Soal 1
Tentukan kedudukan titik \((2, -3)\) terhadap lingkaran-lingkaran berikut:
A. \(x^2 + y^2 = 9\)
B. \((x\:-\:3)^2 + (y\:-\:4)^2 = 50\)
C. \(x^2 + y^2 + 3x\:-\:2y + 5 = 0\)
A. Kedudukan titik \((2, -3)\) terhadap lingkaran \(x^2 + y^2 = 9\)
\(\text{K} = x^2 + y^2 \:-\: 9\)
\(\text{K} = 2^2 + (-3)^2 \:-\: 9\)
\(\text{K} = 4 + 9 \:-\: 9\)
\(\text{K} = 4 < 0\)
Karena \(\text{K} < 0\) maka titik \((2, -3)\) berada di dalam lingkaran \(x^2 + y^2 = 9\)
B. Kedudukan titik \((2, -3)\) terhadap lingkaran \((x\:-\:3)^2 + (y\:-\:4)^2 = 50\)
\(\text{K} = (x\:-\:3)^2 + (y\:-\:4)^2 \:-\: 50\)
\(\text{K} = (2\:-\:3)^2 + (-3\:-\:4)^2 \:-\: 50\)
\(\text{K} = (-1)^2 + (-7)^2 \:-\: 50\)
\(\text{K} = 1 + 49 \:-\: 50\)
\(\text{K} = 0\)
Karena \(\text{K} = 0\) maka titik \((2, -3)\) berada pada lingkaran \((x\:-\:3)^2 + (y\:-\:4)^2 = 50\)
C. Kedudukan titik \((2, -3)\) terhadap lingkaran \(x^2 + y^2 + 3x\:-\:2y + 5 = 0\)
\(\text{K} = x^2 + y^2 + 3x\:-\:2y + 5 \)
\(\text{K} = 2^2 + (-3)^2 + 3(2)\:-\:2(-3) + 5\)
\(\text{K} = 4 + 9 + 6 + 6 +5\)
\(\text{K} = 30\)
\(\text{K} > 0\)
Karena \(\text{K} > 0\) maka titik \((2, -3)\) berada di luar lingkaran \(x^2 + y^2 + 3x\:-\:2y + 5 = 0\)
Soal 2
Tentukan jarak terdekat dan jarak terjauh titik A(3, 3) terhadap lingkaran \(x^2 + y^2 \:-\:2x + 2y\:-\:2 = 0\)
Mengambar lingkaran \(x^2 + y^2 \:-\:2x + 2y\:-\:2 = 0\)
Pusat = \([-\frac{1}{2}(-2), -\frac{1}{2}(2)]\)
Pusat = \((1, -1)\)
Jari-jari = \(\sqrt{1^2 + (-1)^2\:-\:(-2)}\)
Jari-jari = \(\sqrt{1 + 1 + 2}\)
Jari-jari = \(\sqrt{4} = 2\)
Menentukan jarak terdekat
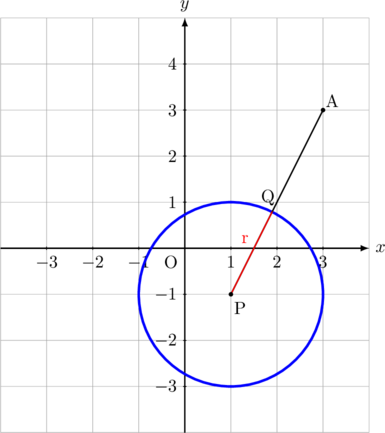
jarak terdekat titik A(3, 3) terhadap lingkaran \(x^2 + y^2 \:-\:2x + 2y\:-\:2 = 0\) adalah panjang AQ.
\(\text{AQ} = \text{AP}\:-\:r\)
dengan AP adalah jarak titik A(3, 3) ke pusat lingkaran P(1, -1)
\(\text{AQ} = \sqrt{(x_2\:-\:x_1)^2 + (y_2\:-\:y_1)^2}\:-\:r\)
\(\text{AQ} = \sqrt{(1\:-\:3)^2 + (-1\:-\:3)^2}\:-\:2\)
\(\text{AQ} = \sqrt{(-2)^2 + (-4)^2}\:-\:2\)
\(\text{AQ} = \sqrt{4 + 16}\:-\:2\)
\(\text{AQ} = \sqrt{20}\:-\:2\)
\(\text{AQ} = 2\sqrt{5}\:-\:2\)
Jadi jarak terdekatnya adalah \(2\sqrt{5}\:-\:2\text{ satuan}\)
Menentukan jarak terjauh
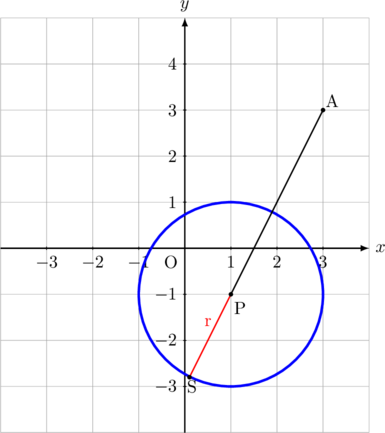
jarak terjauh titik A(3, 3) terhadap lingkaran \(x^2 + y^2 \:-\:2x + 2y\:-\:2 = 0\) adalah panjang AS.
\(\text{AS} = \text{AP} + r\)
\(\text{AS} = 2\sqrt{5} + 2\)
Jadi jarak terjauhnya adalah \(2\sqrt{5} + 2\text{ satuan}\)
Soal 3
Tentukan jarak terdekat dan jarak terjauh titik A(2, 1) terhadap lingkaran \(x^2 + y^2\:-\:2y\:-\:8 = 0\).
Mengambar lingkaran \(x^2 + y^2\:-\:2y\:-\:8 = 0\)
Pusat = \([-\frac{1}{2}(0), -\frac{1}{2}(-2)]\)
Pusat = \((0, 1)\)
Jari-jari = \(\sqrt{0^2 + 1^2\:-\:(-8)}\)
Jari-jari = \(\sqrt{0 + 1 + 8}\)
Jari-jari = \(\sqrt{9} = 3\)
Menentukan jarak terdekat
jarak terdekat titik A(2, 1) terhadap lingkaran \(x^2 + y^2\:-\:2y\:-\:8 = 0\) adalah panjang AQ.
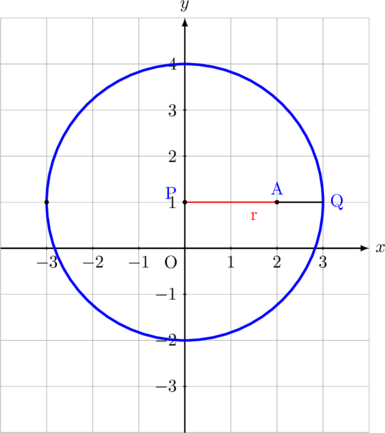
\(\text{AQ} = r\:-\:\text{AP}\)
dengan AP adalah jarak titik A(2, 1) ke pusat lingkaran P(0, 1)
\(\text{AQ} = r\:-\:\sqrt{(x_2\:-\:x_1)^2 + (y_2\:-\:y_1)^2}\)
\(\text{AQ} = 3\:-\:\sqrt{(0\:-\:2)^2 + (1\:-\:1)^2}\)
\(\text{AQ} = 3\:-\:\sqrt{(-2)^2 + 0^2}\)
\(\text{AQ} = 3\:-\:\sqrt{4}\)
\(\text{AQ} = 3\:-\:2\)
\(\text{AQ} = 1 \text{ satuan}\)
Jadi jarak terdekatnya adalah 1 satuan
Menentukan jarak terjauh
jarak terjauh titik A(2, 1) terhadap lingkaran \(x^2 + y^2\:-\:2y\:-\:8 = 0\) adalah panjang AS.
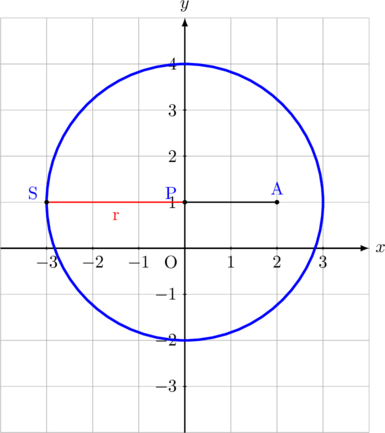
\(\text{AS} = \text{AP} + r\)
\(\text{AS} = 2 + 3\)
\(\text{AS} = 3 \text{ satuan}\)
