Quiz-summary
0 of 20 questions completed
Questions:
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
Information
Dear Students,
Welcome to today’s quiz! This is your opportunity to demonstrate what you’ve learned so far, so do your best. Please keep in mind that you have a maximum of 120 minutes to complete all the questions. Make sure to manage your time wisely and answer each question thoughtfully.
Good luck!
You have already completed the quiz before. Hence you can not start it again.
Quiz is loading...
You must sign in or sign up to start the quiz.
You have to finish following quiz, to start this quiz:
Results
0 of 20 questions answered correctly
Your time:
Time has elapsed
You have reached 0 of 0 points, (0)
Categories
- Not categorized 0%
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- Answered
- Review
-
Question 1 of 20
1. Question
1 pointsYang merupakan persamaan lingkaran adalah…
Correct
\(3x^2 + 3y^2 \:-\:6x + 12y = 36\)
kedua ruas dibagi 3
\(x^2 + y^2 \:-\:2x + 4y = 12\)
\(x^2 + y^2 \:-\:2x + 4y \:-\:12 = 0\)
Persamaan lingkaran dengan pusat (1, -2) dan berjari-jari \(\sqrt{17}\)
Incorrect
\(3x^2 + 3y^2 \:-\:6x + 12y = 36\)
kedua ruas dibagi 3
\(x^2 + y^2 \:-\:2x + 4y = 12\)
\(x^2 + y^2 \:-\:2x + 4y \:-\:12 = 0\)
Persamaan lingkaran dengan pusat (1, -2) dan berjari-jari \(\sqrt{17}\)
-
Question 2 of 20
2. Question
1 pointsPersamaan lingkaran yang berpusat di O(0, 0) dan melalui titik (1, 3) adalah…
Correct
Persamaan lingkaran yang berpusat di O(0, 0) adalah \(x^2 + y^2 = r^2\) selanjutnya untuk mencari jari-jari substitusikan titik (1, 3).
\(1^2 + 3^2 = r^2\)
\(1 + 9 = r^2\)
\(r^2 = 10\)
\(r = \sqrt{10}\)
Jadi persamaan lingkarannya adalah \(x^2 + y^2 = 10\)
Incorrect
Persamaan lingkaran yang berpusat di O(0, 0) adalah \(x^2 + y^2 = r^2\) selanjutnya untuk mencari jari-jari substitusikan titik (1, 3).
\(1^2 + 3^2 = r^2\)
\(1 + 9 = r^2\)
\(r^2 = 10\)
\(r = \sqrt{10}\)
Jadi persamaan lingkarannya adalah \(x^2 + y^2 = 10\)
-
Question 3 of 20
3. Question
1 pointsPersamaan lingkaran yang berpusat di P(3, 5) dan berjari-jari 4 adalah…
Correct
Persamaan lingkaran yang berpusat di titik P(3, 5) dan berjari-jari 4 adalah:
\((x \:-\:a)^2 + (y\:-\:b)^2 = r^2\)
\((x \:-\:3)^2 + (y\:-\:5)^2 = 4^2\)
\(x^2 \:-\:6x + 9 + y^2 \:-\:10y + 25 = 16\)
\(x^2 + y^2 \:-\:6x \:-\:10y + 18 = 0\)
Incorrect
Persamaan lingkaran yang berpusat di titik P(3, 5) dan berjari-jari 4 adalah:
\((x \:-\:a)^2 + (y\:-\:b)^2 = r^2\)
\((x \:-\:3)^2 + (y\:-\:5)^2 = 4^2\)
\(x^2 \:-\:6x + 9 + y^2 \:-\:10y + 25 = 16\)
\(x^2 + y^2 \:-\:6x \:-\:10y + 18 = 0\)
-
Question 4 of 20
4. Question
1 pointsJika persamaan \(3x^2 + y^2 + k(y\:-\:3)^2 + 6x = 15k\) merupakan persamaan lingkaran dengan pusat \(\text{P}(a, b)\) dan berjari-jari \(r\), maka \(a + b + r= \dotso\)
Correct
\(3x^2 + y^2 + k(y\:-\:3)^2 + 6x = 15k\)
\(3x^2 + y^2 + k(y^2 \:-\:6y + 9) + 6x\:-\: 15k = 0\)
\(3x^2 + y^2 + ky^2\:-\:6ky + 9k + 6x\:-\:15k = 0\)
\(3x^2 + (1 + k) y^2\:-\:6ky + 6x\:-\:6k = 0\)
Agar persamaan di atas menjadi persamaan lingkaran, maka koefisien \(x^2\) harus sama dengan koefisien \(y^2\).
\(3 = 1 + k\)
\(k = 2\)
\(3x^2 + 3 y^2 + 6x\:-\:12y \:-\:12= 0\)
Bagi kedua ruas dengan 3,
\(x^2 + y^2 + 2x \:-\:4y \:-\:4 = 0\)
Pusat lingkaran = \(\left(-\dfrac{1}{2}A, -\dfrac{1}{2}B\right)\)
Pusat lingkaran = \(\left(-\dfrac{1}{2}(2), -\dfrac{1}{2}(-4)\right)\)
Pusat lingkaran = \((-1, 2)\)
Jari-jari = \(\sqrt{(-1)^2 + 2^2 \:-\: (-4)}\)
Jari-jari = \(\sqrt{1 + 4 + 4} = \sqrt{9} = 3\)
\(a + b + r = -1 + 2 + 3 = 4\)
Incorrect
\(3x^2 + y^2 + k(y\:-\:3)^2 + 6x = 15k\)
\(3x^2 + y^2 + k(y^2 \:-\:6y + 9) + 6x\:-\: 15k = 0\)
\(3x^2 + y^2 + ky^2\:-\:6ky + 9k + 6x\:-\:15k = 0\)
\(3x^2 + (1 + k) y^2\:-\:6ky + 6x\:-\:6k = 0\)
Agar persamaan di atas menjadi persamaan lingkaran, maka koefisien \(x^2\) harus sama dengan koefisien \(y^2\).
\(3 = 1 + k\)
\(k = 2\)
\(3x^2 + 3 y^2 + 6x\:-\:12y \:-\:12= 0\)
Bagi kedua ruas dengan 3,
\(x^2 + y^2 + 2x \:-\:4y \:-\:4 = 0\)
Pusat lingkaran = \(\left(-\dfrac{1}{2}A, -\dfrac{1}{2}B\right)\)
Pusat lingkaran = \(\left(-\dfrac{1}{2}(2), -\dfrac{1}{2}(-4)\right)\)
Pusat lingkaran = \((-1, 2)\)
Jari-jari = \(\sqrt{(-1)^2 + 2^2 \:-\: (-4)}\)
Jari-jari = \(\sqrt{1 + 4 + 4} = \sqrt{9} = 3\)
\(a + b + r = -1 + 2 + 3 = 4\)
-
Question 5 of 20
5. Question
1 pointsTempat kedudukan titik-titik yang jaraknya terhadap titik A(0, 5) dua kali jaraknya terhadap titik B(0, −2) adalah…
Correct
Misal titik tersebut adalah \(\text{P}(x, y)\)
Jarak titik P(x, y) ke titik A(0, 5) sama dengan dua kali jarak titik P(x, y) ke titik B(0, −2)
\(\text{PA} = 2\cdot \text{PB}\)
\(\sqrt{(x\:-\:0)^2 + (y\:-\:5)^2} = 2 \sqrt{(x\:-\:0)^2 + (y\:-\:(-2))^2}\)
Selanjutnya kuadratkan kedua ruas
\(x^2 + y^2 \:-\:10y + 25 = 4(x^2 + y^2 + 4y + 4)\)
\(x^2 + y^2 \:-\:10y + 25 = 4x^2 + 4y^2 + 16y + 16\)
\(3x^2 + 3y^2 + 26y \:-\:9 = 0\)
Incorrect
Misal titik tersebut adalah \(\text{P}(x, y)\)
Jarak titik P(x, y) ke titik A(0, 5) sama dengan dua kali jarak titik P(x, y) ke titik B(0, −2)
\(\text{PA} = 2\cdot \text{PB}\)
\(\sqrt{(x\:-\:0)^2 + (y\:-\:5)^2} = 2 \sqrt{(x\:-\:0)^2 + (y\:-\:(-2))^2}\)
Selanjutnya kuadratkan kedua ruas
\(x^2 + y^2 \:-\:10y + 25 = 4(x^2 + y^2 + 4y + 4)\)
\(x^2 + y^2 \:-\:10y + 25 = 4x^2 + 4y^2 + 16y + 16\)
\(3x^2 + 3y^2 + 26y \:-\:9 = 0\)
-
Question 6 of 20
6. Question
1 pointsPersamaan lingkaran yang berparameter:
\(x = 4 \cos \theta \:-\:2\)
\(y = 4 \sin \theta + 3\)
untuk \(0 \leq \theta \leq 2 \pi\) adalah….
Correct
\(x = a + r \cos \theta\)
\(y = b + r \sin \theta\)
Merupakan lingkaran yang berpusat di \((a, b)\) dan berjari-jari \(r\)
Sehingga untuk persamaan parameter:
\(x = 4 \cos \theta \:-\:2\) dapat ditulis \(x = -2 + 4 \cos \theta\)
\(y = 4 \sin \theta + 3\) dapat ditulis \(y = 3 + 4 \sin \theta\)
merupakan persamaan lingkaran yang berpusat di (-2, 3) dan berjari-jari 4
\((x\:-\:(-2))^2 + (y\:-\:3)^2 = 4^2\)
\(x^2 + 4x + 4 + y^2 \:-\:6y + 9 = 16\)
\(x^2 + y^2 + 4x \:-\:6y \:-\:3 = 0\)
Incorrect
\(x = a + r \cos \theta\)
\(y = b + r \sin \theta\)
Merupakan lingkaran yang berpusat di \((a, b)\) dan berjari-jari \(r\)
Sehingga untuk persamaan parameter:
\(x = 4 \cos \theta \:-\:2\) dapat ditulis \(x = -2 + 4 \cos \theta\)
\(y = 4 \sin \theta + 3\) dapat ditulis \(y = 3 + 4 \sin \theta\)
merupakan persamaan lingkaran yang berpusat di (-2, 3) dan berjari-jari 4
\((x\:-\:(-2))^2 + (y\:-\:3)^2 = 4^2\)
\(x^2 + 4x + 4 + y^2 \:-\:6y + 9 = 16\)
\(x^2 + y^2 + 4x \:-\:6y \:-\:3 = 0\)
-
Question 7 of 20
7. Question
1 pointsLingkaran yang konsentris dengan \(x^2 + y^2 + 8x \:-\:10y \:-\:8= 0\) namun jari-jarinya dua kalinya adalah…
Correct
Konsentris artinya sepusat
\(\text{L}_1 : x^2 + y^2 + 8x \:-\:10y \:-\:8= 0\)
Pusat lingkarannya \((-\frac{1}{2}(8), -\frac{1}{2}(-10)) = (-4, 5)\)
Jari-jari lingkaran L1 adalah \(\sqrt{(-4)^2 + 5^2 \:-\:(-8)} = \sqrt{49} = 7\)
Lingkaran yang dicari adalah L2
Pusatnya sama dengan L1 yaitu \((-4, 5)\) sedangkan jari-jarinya \(2 \times 7 = 14\)
Persamaan lingkaran L2 adalah:
\((x + 4)^2 + (y \:-\:5)^2 = 14^2\)
\(x^2 + 8x + 16 + y^2 \:-\:10y + 25 = 196\)
\(x^2 + y^2 + 8x \:-\:10y \:-\:155 = 0\)
Incorrect
Konsentris artinya sepusat
\(\text{L}_1 : x^2 + y^2 + 8x \:-\:10y \:-\:8= 0\)
Pusat lingkarannya \((-\frac{1}{2}(8), -\frac{1}{2}(-10)) = (-4, 5)\)
Jari-jari lingkaran L1 adalah \(\sqrt{(-4)^2 + 5^2 \:-\:(-8)} = \sqrt{49} = 7\)
Lingkaran yang dicari adalah L2
Pusatnya sama dengan L1 yaitu \((-4, 5)\) sedangkan jari-jarinya \(2 \times 7 = 14\)
Persamaan lingkaran L2 adalah:
\((x + 4)^2 + (y \:-\:5)^2 = 14^2\)
\(x^2 + 8x + 16 + y^2 \:-\:10y + 25 = 196\)
\(x^2 + y^2 + 8x \:-\:10y \:-\:155 = 0\)
-
Question 8 of 20
8. Question
1 pointsPersamaan garis singgung lingkaran \(x^2 + y^2 \:-\:6x + 4y \:-\:12=0\) di titik \((7, 1)\) adalah…
Correct
Kuasa titik \((7, 1)\) terhadap lingkaran:
\(\text{K} = x^2 + y^2 \:-\:6x + 4y \:-\:12\)
\(\text{K} = 7^2 + 1^2 \:-\:6(7) + 4(1) \:-\:12\)
\(\text{K} = 0\)
Karena kuasa sama dengan nol, maka titik \((7, 1)\) terletak pada lingkaran dan selanjutnya disebut dengan titik singgung lingkaran.
Persamaan garis singgung di titik \((7, 1)\) adalah:
\(x_1\cdot x + y_1 \cdot y + \dfrac{1}{2}(-6)(x_1 + x) + \dfrac{1}{2}(4)(y_1 + y) \:-\:12 = 0\)
\(7x + y + (-3)(7 + x) + (2)(1+ y) \:-\:12 = 0\)
\(7x + y \:-\:21 \:-\:3x + 2 + 2y\:-\:12 = 0\)
\(4x + 3y \:-\:31 = 0\)
Incorrect
Kuasa titik \((7, 1)\) terhadap lingkaran:
\(\text{K} = x^2 + y^2 \:-\:6x + 4y \:-\:12\)
\(\text{K} = 7^2 + 1^2 \:-\:6(7) + 4(1) \:-\:12\)
\(\text{K} = 0\)
Karena kuasa sama dengan nol, maka titik \((7, 1)\) terletak pada lingkaran dan selanjutnya disebut dengan titik singgung lingkaran.
Persamaan garis singgung di titik \((7, 1)\) adalah:
\(x_1\cdot x + y_1 \cdot y + \dfrac{1}{2}(-6)(x_1 + x) + \dfrac{1}{2}(4)(y_1 + y) \:-\:12 = 0\)
\(7x + y + (-3)(7 + x) + (2)(1+ y) \:-\:12 = 0\)
\(7x + y \:-\:21 \:-\:3x + 2 + 2y\:-\:12 = 0\)
\(4x + 3y \:-\:31 = 0\)
-
Question 9 of 20
9. Question
1 pointsLingkaran \((x + 1)^2 + (y\:-\:3)^2 = 9\) memotong garis \(y = 3\). Garis singgung lingkaran yang melalui titik potong antara lingkaran dan garis tersebut adalah…
Correct
Langkah 1: Menentukan titik singgung
Substitusikan garis \(y = 3\) ke persamaan lingkaran\((x + 1)^2 + (y\:-\:3)^2 = 9\).
\((x + 1)^2 + (3\:-\:3)^2 = 9\)
\((x + 1)^2 + 0 = 9\)
\(x + 1 = \pm \sqrt{9}\)
\(x_1 = +3\:-\:1 = 2\)
\(x_2= -3 \:-\:1 = -4\)
Titik singgungnnya berada di \((2, 3)\) dan \((-4, 3)\)
Langkah 2: Menentukan persamaan garis singgung
Persamaan garis singgung di titik \((2, 3)\):
\((x_1 + 1)(x + 1) + (y_1 \:-\:3)(y \:-\:3) = 9\)
\((2 + 1)(x + 1) + (3 \:-\:3)(y \:-\:3) = 9\)
\(3x + 3 + 0= 9\)
\(3x = 6\)
\(x = 2\)
Persamaan garis singgung di titik \((-4, 3)\):
\((x_1 + 1)(x + 1) + (y_1 \:-\:3)(y \:-\:3) = 9\)
\((-4 + 1)(x + 1) + (3 \:-\:3)(y \:-\:3) = 9\)
\(-3x\:-\:3 = 9\)
\(-3x = 12\)
\(x = -4\)
Incorrect
Langkah 1: Menentukan titik singgung
Substitusikan garis \(y = 3\) ke persamaan lingkaran\((x + 1)^2 + (y\:-\:3)^2 = 9\).
\((x + 1)^2 + (3\:-\:3)^2 = 9\)
\((x + 1)^2 + 0 = 9\)
\(x + 1 = \pm \sqrt{9}\)
\(x_1 = +3\:-\:1 = 2\)
\(x_2= -3 \:-\:1 = -4\)
Titik singgungnnya berada di \((2, 3)\) dan \((-4, 3)\)
Langkah 2: Menentukan persamaan garis singgung
Persamaan garis singgung di titik \((2, 3)\):
\((x_1 + 1)(x + 1) + (y_1 \:-\:3)(y \:-\:3) = 9\)
\((2 + 1)(x + 1) + (3 \:-\:3)(y \:-\:3) = 9\)
\(3x + 3 + 0= 9\)
\(3x = 6\)
\(x = 2\)
Persamaan garis singgung di titik \((-4, 3)\):
\((x_1 + 1)(x + 1) + (y_1 \:-\:3)(y \:-\:3) = 9\)
\((-4 + 1)(x + 1) + (3 \:-\:3)(y \:-\:3) = 9\)
\(-3x\:-\:3 = 9\)
\(-3x = 12\)
\(x = -4\)
-
Question 10 of 20
10. Question
1 pointsPersamaan garis singgung lingkaran \(x^2 + y^2 = 5\) yang melalui titik \((-5, 5)\) adalah…
Correct
Langkah 1: Menentukan persamaan garis polar
\(x_1\cdot x + y_1 \cdot y = 5\)
Selanjutnya substitusikan titik \((-5, 5)\)
\(-5x + 5y = 5\)
\(-x + y = 1\)
\(y = x + 1\)
Langkah 2: Menentukan titik singgung
Substitusikan \(y = x + 1\) ke persamaan lingkaran \(x^2 + y^2 = 5\)
\(x^2 + (x + 1)^2 = 5\)
\(x^2 + x^2 + 2x + 1 = 5\)
\(2x^2 + 2x\:-\:4 = 0\)
Bagi kedua ruas dengan 2
\(x^2 + x\:-\:2 = 0\)
\((x + 2)(x\:-\:1) = 0\)
\(x + 2 = 0 \rightarrow x_1 = -2\)
\(x\:-\:1 = 0 \rightarrow x_2 = 1\)
Untuk \(x_1 = -2\) maka \(y_1 = -1\)
Untuk \(x_2 = 1\) maka \(y_2 = 2\)
Langkah 3: Menentukan persamaan garis singgung lingkaran
Persamaan garis singgung di titik \((-2, -1)\) adalah:
\(x_1 \cdot x + y_1 \cdot y = 5\)
\(-2x\:-\:y = 5\)
Persamaan garis singgung di titik \((1, 2)\) adalah:
\(x_2\cdot x + y_2\cdot y = 5\)
\(x + 2y = 5\)
Incorrect
Langkah 1: Menentukan persamaan garis polar
\(x_1\cdot x + y_1 \cdot y = 5\)
Selanjutnya substitusikan titik \((-5, 5)\)
\(-5x + 5y = 5\)
\(-x + y = 1\)
\(y = x + 1\)
Langkah 2: Menentukan titik singgung
Substitusikan \(y = x + 1\) ke persamaan lingkaran \(x^2 + y^2 = 5\)
\(x^2 + (x + 1)^2 = 5\)
\(x^2 + x^2 + 2x + 1 = 5\)
\(2x^2 + 2x\:-\:4 = 0\)
Bagi kedua ruas dengan 2
\(x^2 + x\:-\:2 = 0\)
\((x + 2)(x\:-\:1) = 0\)
\(x + 2 = 0 \rightarrow x_1 = -2\)
\(x\:-\:1 = 0 \rightarrow x_2 = 1\)
Untuk \(x_1 = -2\) maka \(y_1 = -1\)
Untuk \(x_2 = 1\) maka \(y_2 = 2\)
Langkah 3: Menentukan persamaan garis singgung lingkaran
Persamaan garis singgung di titik \((-2, -1)\) adalah:
\(x_1 \cdot x + y_1 \cdot y = 5\)
\(-2x\:-\:y = 5\)
Persamaan garis singgung di titik \((1, 2)\) adalah:
\(x_2\cdot x + y_2\cdot y = 5\)
\(x + 2y = 5\)
-
Question 11 of 20
11. Question
1 pointsPersamaan lingkaran yang berpusat di titik \(\text{P}(-3, 7)\) dan melalui titik \(\text{R}(2, -5)\) adalah…
Correct
Jari-jari lingkaran merupakan jarak titik \(\text{P}(-3, 7)\) ke titik \(\text{R}(2, -5)\)
\(r = \sqrt{(2 + 3)^2 + (-5\:-\:7)^2}\)
\(r = \sqrt{25 + 144}\)
\(r = \sqrt{169} = 13\)
Persamaan lingkaran berpusat di \(\text{P}(-3, 7)\) dan berjari-jari 13 adalah:
\((x\:-\:a)^2 + (y\:-\:b)^2 = r^2\)
\((x + 3)^2 + (y\:-\:7)^2 = 13^2\)
\(x^2 + 6x + 9 + y^2 \:-\:14y + 49 = 169\)
\(x^2 + y^2 + 6x\:-\:14y \:-\:111 = 0\)
Incorrect
Jari-jari lingkaran merupakan jarak titik \(\text{P}(-3, 7)\) ke titik \(\text{R}(2, -5)\)
\(r = \sqrt{(2 + 3)^2 + (-5\:-\:7)^2}\)
\(r = \sqrt{25 + 144}\)
\(r = \sqrt{169} = 13\)
Persamaan lingkaran berpusat di \(\text{P}(-3, 7)\) dan berjari-jari 13 adalah:
\((x\:-\:a)^2 + (y\:-\:b)^2 = r^2\)
\((x + 3)^2 + (y\:-\:7)^2 = 13^2\)
\(x^2 + 6x + 9 + y^2 \:-\:14y + 49 = 169\)
\(x^2 + y^2 + 6x\:-\:14y \:-\:111 = 0\)
-
Question 12 of 20
12. Question
1 pointsPanjang jari-jari lingkaran \(x^2 + y^2 + 6x\:-\:10y + 18 = 0\) adalah…
Correct
\(x^2 + y^2 + 6x\:-\:10y + 18 = 0\)
Pusat lingkaran \((-3, 5)\)
Jari-jari lingkaran = \(\sqrt{(-3)^2 + 5^2\:-\:18}\)
Jari-jari lingkaran = \(\sqrt{16} = 4\)
Incorrect
\(x^2 + y^2 + 6x\:-\:10y + 18 = 0\)
Pusat lingkaran \((-3, 5)\)
Jari-jari lingkaran = \(\sqrt{(-3)^2 + 5^2\:-\:18}\)
Jari-jari lingkaran = \(\sqrt{16} = 4\)
-
Question 13 of 20
13. Question
1 pointsPersamaan lingkaran yang mempunyai diameter AB dimana \(\text{A}(-2, 4)\) dan \(\text{B}(2, -4)\) adalah…
Correct
Pusat lingkaran terletak di titik tengah ruas garis AB dimana \(\text{A}(-2, 4)\) dan \(\text{B}(2, -4)\).
\(\text{P}\left(\dfrac{x_1 + x_2}{2}, \dfrac{y_1 + y_2}{2}\right)\)
\(\text{P}\left(\dfrac{-2 + 2}{2}, \dfrac{4 \:-\:4}{2}\right)\)
\(\text{P}(0, 0)\)
Jari-jari lingkaran adalah jarak titik pusat ke titik A atau titik B
Jarak titik \(\text{P}(0, 0)\) ke titik \(\text{B}(2, -4)\) adalah:
\(r = \sqrt{(2\:-\:0)^2 + (-4\:-\:0)^2}\)
\(r = \sqrt{20}\)
Persamaan lingkaran yang berpusat di titik (0, 0) dan berjari-jari \(r = \sqrt{20}\) adalah:
\(x^2 + y^2 = 20\)
Incorrect
Pusat lingkaran terletak di titik tengah ruas garis AB dimana \(\text{A}(-2, 4)\) dan \(\text{B}(2, -4)\).
\(\text{P}\left(\dfrac{x_1 + x_2}{2}, \dfrac{y_1 + y_2}{2}\right)\)
\(\text{P}\left(\dfrac{-2 + 2}{2}, \dfrac{4 \:-\:4}{2}\right)\)
\(\text{P}(0, 0)\)
Jari-jari lingkaran adalah jarak titik pusat ke titik A atau titik B
Jarak titik \(\text{P}(0, 0)\) ke titik \(\text{B}(2, -4)\) adalah:
\(r = \sqrt{(2\:-\:0)^2 + (-4\:-\:0)^2}\)
\(r = \sqrt{20}\)
Persamaan lingkaran yang berpusat di titik (0, 0) dan berjari-jari \(r = \sqrt{20}\) adalah:
\(x^2 + y^2 = 20\)
-
Question 14 of 20
14. Question
1 pointsPersamaan lingkaran yang melalui titik \(\text{P}(4, 2)\), \(\text{Q}(-3, -5)\), dan \(\text{R}(5, 1)\) adalah…
Correct
Persamaan umum lingkaran: \(x^2 + y^2 + Ax + By + C = 0\)
Substitusikan titik P, Q, dan R ke dalam persamaan umum lingkaran tersebut, kemudian eliminasikan ketiga persamaan untuk mendapatkan nilai A, B, dan C.
Titik \(\text{P}(4, 2)\)
\(4^2 + 2^2 + 4A + 2B + C = 0\)
\(20 + 4A + 2B + C = 0 \dotso \color{red} (1)\)
Titik \(\text{Q}(-3, -5)\)
\((-3)^2 + (-5)^2 \:-\:3A\:-\:5B + C = 0\)
\(34\:-\:3A\:-\:5B + C = 0 \dotso \color{red} (2)\)
Titik \(\text{R}(5, 1)\)
\((5)^2 + 1^2 + 5A + B + C = 0\)
\(26 + 5A + B + C = 0\dotso \color{red} (3)\)
Hasil eliminasi ketiga persamaan di atas akan memperoleh nilai \(A = -2, B = 4, \text{ dan } C = -20\), sehingga persamaan lingkarannya adalah:
\(x^2 + y^2 \:-\:2x + 4y \:-\:20 = 0\)
Incorrect
Persamaan umum lingkaran: \(x^2 + y^2 + Ax + By + C = 0\)
Substitusikan titik P, Q, dan R ke dalam persamaan umum lingkaran tersebut, kemudian eliminasikan ketiga persamaan untuk mendapatkan nilai A, B, dan C.
Titik \(\text{P}(4, 2)\)
\(4^2 + 2^2 + 4A + 2B + C = 0\)
\(20 + 4A + 2B + C = 0 \dotso \color{red} (1)\)
Titik \(\text{Q}(-3, -5)\)
\((-3)^2 + (-5)^2 \:-\:3A\:-\:5B + C = 0\)
\(34\:-\:3A\:-\:5B + C = 0 \dotso \color{red} (2)\)
Titik \(\text{R}(5, 1)\)
\((5)^2 + 1^2 + 5A + B + C = 0\)
\(26 + 5A + B + C = 0\dotso \color{red} (3)\)
Hasil eliminasi ketiga persamaan di atas akan memperoleh nilai \(A = -2, B = 4, \text{ dan } C = -20\), sehingga persamaan lingkarannya adalah:
\(x^2 + y^2 \:-\:2x + 4y \:-\:20 = 0\)
-
Question 15 of 20
15. Question
1 pointsSalah satu persamaan lingkaran yang berjari-jari 3 dan menyinggung lingkaran \(x^2 + y^2 \:-\:4x \:-\:6y \:-\:12 = 0\) di titik yang berabsis 6 adalah…
Correct
Substitusikan \(x = 6\) ke lingkaran \(x^2 + y^2 \:-\:4x \:-\:6y \:-\:12 = 0\) untuk mendapatkan titik singgung.
\(6^2 + y^2 \:-\:4(6)\:-\:6y \:-\:12 = 0\)
\(36 + y^2 \:-\:24\:-\:6y \:-\:12 = 0\)
\(y^2 \:-\:6y = 0\)
\(y(y\:-\:6) = 0\)
didapat \(y = 0 \text{ atau } y = 6\)
Titik singung berada di \((6, 0)\) atau \((6, 6)\)
Perhatikan gambar berikut
Misal lingkaran yang dicari berpusat di \((a, b)\)

Dengan menggunakan perbandingan ruas garis, pusat lingkaran \((a, b)\) dapat ditemukan.
\(6 = \dfrac{3(2) + 5a}{3 + 5}\)
\(48 = 6 + 5a\)
\(a = \dfrac{42}{5}\)
\(6 = \dfrac{3(3) + 5b}{3 + 5}\)
\(48 = 9 + 5b\)
\(b = \dfrac{39}{5}\)
Persamaan lingkaran yang berpusat di \(\left(\dfrac{42}{5}, \dfrac{39}{5}\right)\) dan berjari-jari 3 adalah:
\(\left(x\:-\:\dfrac{42}{5}\right)^2 + \left(y\:-\:\dfrac{39}{5}\right)^2 = 3^2\)
\(\left(x\:-\:\dfrac{42}{5}\right)^2 + \left(y\:-\:\dfrac{39}{5}\right)^2 = 9\)
Incorrect
Substitusikan \(x = 6\) ke lingkaran \(x^2 + y^2 \:-\:4x \:-\:6y \:-\:12 = 0\) untuk mendapatkan titik singgung.
\(6^2 + y^2 \:-\:4(6)\:-\:6y \:-\:12 = 0\)
\(36 + y^2 \:-\:24\:-\:6y \:-\:12 = 0\)
\(y^2 \:-\:6y = 0\)
\(y(y\:-\:6) = 0\)
didapat \(y = 0 \text{ atau } y = 6\)
Titik singung berada di \((6, 0)\) atau \((6, 6)\)
Perhatikan gambar berikut
Misal lingkaran yang dicari berpusat di \((a, b)\)

Dengan menggunakan perbandingan ruas garis, pusat lingkaran \((a, b)\) dapat ditemukan.
\(6 = \dfrac{3(2) + 5a}{3 + 5}\)
\(48 = 6 + 5a\)
\(a = \dfrac{42}{5}\)
\(6 = \dfrac{3(3) + 5b}{3 + 5}\)
\(48 = 9 + 5b\)
\(b = \dfrac{39}{5}\)
Persamaan lingkaran yang berpusat di \(\left(\dfrac{42}{5}, \dfrac{39}{5}\right)\) dan berjari-jari 3 adalah:
\(\left(x\:-\:\dfrac{42}{5}\right)^2 + \left(y\:-\:\dfrac{39}{5}\right)^2 = 3^2\)
\(\left(x\:-\:\dfrac{42}{5}\right)^2 + \left(y\:-\:\dfrac{39}{5}\right)^2 = 9\)
-
Question 16 of 20
16. Question
1 pointsPerhatikan gambar berikut!
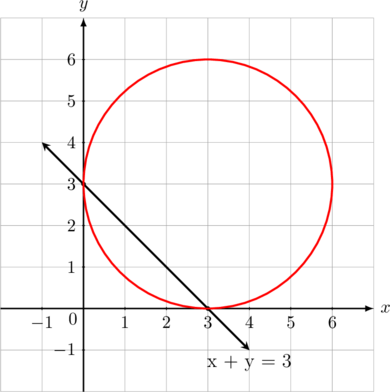
Persamaan lingkaran di atas adalah…
Correct
Dari gambar terlihat bahwa lingkaran menyinggung sumbu Y di titik (0, 3) dan menyinggung sumbu X di titik (3, 0). Pusat lingkaran berada pada titik (3, 3) dan berjari-jari 3.
Persamaan lingkarannya adalah:
\((x\:-\:3)^2 + (y\:-\:3)^2 = 3^2\)
\(x^2 \:-\:6x + 9 + y^2 \:-\:6y + 9 = 9\)
\(x^2 + y^2 \:-\:6x\:-\:6y + 9 = 0\)
Incorrect
Dari gambar terlihat bahwa lingkaran menyinggung sumbu Y di titik (0, 3) dan menyinggung sumbu X di titik (3, 0). Pusat lingkaran berada pada titik (3, 3) dan berjari-jari 3.
Persamaan lingkarannya adalah:
\((x\:-\:3)^2 + (y\:-\:3)^2 = 3^2\)
\(x^2 \:-\:6x + 9 + y^2 \:-\:6y + 9 = 9\)
\(x^2 + y^2 \:-\:6x\:-\:6y + 9 = 0\)
-
Question 17 of 20
17. Question
1 pointsPerhatikan gambar berikut!
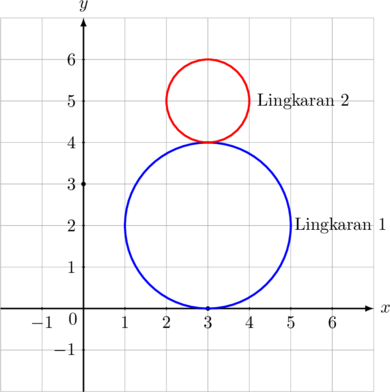
Jika persamaan lingkaran 1 adalah \(x^2 + y^2 \:-\:6x\:-\:4y + 9 = 0\), maka persamaan lingkaran 2 adalah…
Correct
Lingkaran 2 berpusat di \((3, 5)\) dan berjari-jari 1
Persamaan lingkaran 2 adalah:
\((x\:-\:3)^2 + (y\:-\:5)^2 = 1^2\)
\(x^2 \:-\:6x + 9 + y^2 \:-\:10y + 25 = 1\)
\(x^2 + y^2 \:-\:6x \:-\:10y + 33= 0\)
Incorrect
Lingkaran 2 berpusat di \((3, 5)\) dan berjari-jari 1
Persamaan lingkaran 2 adalah:
\((x\:-\:3)^2 + (y\:-\:5)^2 = 1^2\)
\(x^2 \:-\:6x + 9 + y^2 \:-\:10y + 25 = 1\)
\(x^2 + y^2 \:-\:6x \:-\:10y + 33= 0\)
-
Question 18 of 20
18. Question
1 pointsPerhatikan gambar berikut:

Persamaan lingkaran yang berjari-jari \(5\sqrt{13}\) dan memotong sumbu X positif pada suatu segmen garis sepanjang 36 satuan dan memotong sumbu Y positif pada suatu segmen garis sepanjang 20 satuan adalah…
Correct
Perhatikan gambar berikut!
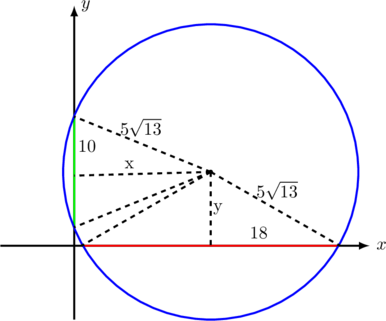
Menentukan nilai \(x\)
\(x^2 + 10^2 = (5\sqrt{13})^2\)
\(x^2 + 100 = 325\)
\(x^2 = 225\)
\(x = \sqrt{225}\)
\(x = 15\)
Menentukan nilai \(y\)
\(y^2 + 18^2 = (5\sqrt{13})^2\)
\(y^2 + 324 = 325\)
\(y^2 = 1\)
\(y = 1\)
Pusat lingkaran berada di titik (15, 1).
Persamaan lingkaran yang berpusat di titik (15, 1) dan berjari-jari \(5\sqrt{13}\) adalah:
\((x\:-\:15)^2 + (y\:-\:1)^2 = (5\sqrt{13})^2\)
\(x^2 \:-\:30x + 225 + y^2 \:-\:2y + 1 = 325\)
\(x^2 + y^2 \:-\:30x\:-\:2y \:-\:99 = 0\)
Incorrect
Perhatikan gambar berikut!

Menentukan nilai \(x\)
\(x^2 + 10^2 = (5\sqrt{13})^2\)
\(x^2 + 100 = 325\)
\(x^2 = 225\)
\(x = \sqrt{225}\)
\(x = 15\)
Menentukan nilai \(y\)
\(y^2 + 18^2 = (5\sqrt{13})^2\)
\(y^2 + 324 = 325\)
\(y^2 = 1\)
\(y = 1\)
Pusat lingkaran berada di titik (15, 1).
Persamaan lingkaran yang berpusat di titik (15, 1) dan berjari-jari \(5\sqrt{13}\) adalah:
\((x\:-\:15)^2 + (y\:-\:1)^2 = (5\sqrt{13})^2\)
\(x^2 \:-\:30x + 225 + y^2 \:-\:2y + 1 = 325\)
\(x^2 + y^2 \:-\:30x\:-\:2y \:-\:99 = 0\)
-
Question 19 of 20
19. Question
1 pointsSalah satu persamaan lingkaran yang berjari-jari 5 satuan, melalui titik asal dan pusatnya terletak pada garis \(x + y \:-\:1 = 0\) adalah…
Correct
Pusat lingkaran terletak pada garis \(y = 1\:-\:x\)
Misalkan pusatnya berada di \(\text{P}(a, 1\:-\:a)\)
Jarak \(\text{P}(a, 1\:-\:a)\) ke titik asal \((0, 0)\) adalah jari-jari lingkaran
\(\text{R} = \sqrt{(a\:-\:0)^2 + (1\:-\:a\:-\:0)^2}\)
\(5 = \sqrt{(a\:-\:0)^2 + (1\:-\:a\:-\:0)^2}\)
Kuadratkan kedua ruas,
\(25 = a^2 + (1\:-\:a)^2\)
\(25 = a^2 + 1\:-\:2a + a^2\)
\(2a^2 \:-\:2a \:-\:24 = 0\)
\(a^2\:-\:a\:-\:12 = 0\)
\((a\:-\:4)(a + 3) = 0\)
\(a = 4 \text{ atau } a = -3\)
Untuk \(a = 4\) maka pusat lingkarannya berada di \((4, -3)\)
Persamaan lingkaran yang berpusat di \((4, -3)\) dan berjari-jari 5 adalah:
\((x\:-\:4)^2 + (y + 3)^2 = 25\)
Incorrect
Pusat lingkaran terletak pada garis \(y = 1\:-\:x\)
Misalkan pusatnya berada di \(\text{P}(a, 1\:-\:a)\)
Jarak \(\text{P}(a, 1\:-\:a)\) ke titik asal \((0, 0)\) adalah jari-jari lingkaran
\(\text{R} = \sqrt{(a\:-\:0)^2 + (1\:-\:a\:-\:0)^2}\)
\(5 = \sqrt{(a\:-\:0)^2 + (1\:-\:a\:-\:0)^2}\)
Kuadratkan kedua ruas,
\(25 = a^2 + (1\:-\:a)^2\)
\(25 = a^2 + 1\:-\:2a + a^2\)
\(2a^2 \:-\:2a \:-\:24 = 0\)
\(a^2\:-\:a\:-\:12 = 0\)
\((a\:-\:4)(a + 3) = 0\)
\(a = 4 \text{ atau } a = -3\)
Untuk \(a = 4\) maka pusat lingkarannya berada di \((4, -3)\)
Persamaan lingkaran yang berpusat di \((4, -3)\) dan berjari-jari 5 adalah:
\((x\:-\:4)^2 + (y + 3)^2 = 25\)
-
Question 20 of 20
20. Question
1 pointsPersamaan lingkaran yang melalui titik \((6, 3)\) dan \((-2, -1)\) dan pusatnya terletak pada garis \(x\:-\:y + 2 = 0\) adalah…
Correct
Misal pusat lingkaran berada di \(\text{P}(a, a + 2)\)
Jarak \(\text{P}(a, a + 2)\) ke titik \((6, 3)\) = jarak \(\text{P}(a, a + 2)\) ke titik \((-2, -1)\)
\(\sqrt{(a\:-\:6)^2 + (a+ 2\:-\:3)^2} = \sqrt{(a + 2)^2 + (a + 2 + 1)^2}\)
\((a\:-\:6)^2 + (a\:-\:1)^2 = (a + 2)^2 + (a + 3)^2\)
\(a^2 \:-\:12a + 36 + a^2 \:-\:2a + 1 = a^2 + 4a + 4 + a^2 + 6a + 9\)
\(-14a + 37 = 10a + 13\)
\(-24a = -24\)
\(a = 1\)
Pusat lingkaran berada di \((1, 3)\)
\(\text{R} = \sqrt{(1\:-\:6)^2 + (1\:-\:1)^2}\)
\(\text{R} = 5\)
Persamaan lingkaran berpusat di \((1, 3)\) dan berjari-jari 5 adalah:
\((x\:-\:1)^2 + (y\:-\:3)^2 = 25\)
Incorrect
Misal pusat lingkaran berada di \(\text{P}(a, a + 2)\)
Jarak \(\text{P}(a, a + 2)\) ke titik \((6, 3)\) = jarak \(\text{P}(a, a + 2)\) ke titik \((-2, -1)\)
\(\sqrt{(a\:-\:6)^2 + (a+ 2\:-\:3)^2} = \sqrt{(a + 2)^2 + (a + 2 + 1)^2}\)
\((a\:-\:6)^2 + (a\:-\:1)^2 = (a + 2)^2 + (a + 3)^2\)
\(a^2 \:-\:12a + 36 + a^2 \:-\:2a + 1 = a^2 + 4a + 4 + a^2 + 6a + 9\)
\(-14a + 37 = 10a + 13\)
\(-24a = -24\)
\(a = 1\)
Pusat lingkaran berada di \((1, 3)\)
\(\text{R} = \sqrt{(1\:-\:6)^2 + (1\:-\:1)^2}\)
\(\text{R} = 5\)
Persamaan lingkaran berpusat di \((1, 3)\) dan berjari-jari 5 adalah:
\((x\:-\:1)^2 + (y\:-\:3)^2 = 25\)
