Soal 01
Lingkaran \(x^2 + y^2 \:-\:14x + 22y + 1 = 0\) mempunyai pusat \((a, b)\) dan jari-jari \(r\), maka \(a + b + 2r = \dotso\)
(A) 21
(B) 22
(C) 23
(D) 24
(E) 25
Answer: B
\(x^2 + y^2 \:-\:14x + 22y + 1 = 0\)
Pusat lingkaran = \(\left(-\dfrac{1}{2}A, -\dfrac{1}{2}B \right)\)
Pusat lingkaran = \(\left(-\dfrac{1}{2}(-14), -\dfrac{1}{2}(22) \right)\)
Pusat lingkaran = \((7, -11)\)
Jari-jari lingkaran = \(\sqrt{7^2 + (-11)^2 \:-\: C}\)
Jari-jari lingkaran = \(\sqrt{49 + 121 \:-\: 1}\)
Jari-jari lingkaran = \(\sqrt{169} = 13\)
\(a + b + 2r = 7\:-\:11 + 2(13)\)
\(a + b + 2r = 22\)
Soal 02
Salah satu persamaan garis singgung pada lingkaran \(x^2 + y^2 \:-\:12x + 4y + 23 =0\) dan tegak lurus dengan garis AB dengan \(\text{A}(2, 7)\) dan \(\text{B}(6, 6)\) adalah…
(A) \(3y \:-\:2x + 5 = 0\)
(B) \(3y \:-\:2x + 7 = 0\)
(C) \(2y + 3x \:-\: 5 = 0\)
(D) \(2x + 3y \:-\:7 = 0\)
(E) \(y \:-\:4x + 9 = 0\)
Answer: E
Mencari gradien garis AB \((m_1)\)
\(m_1 = \dfrac{y_2\:-\:y_1}{x_2 \:-\:x_1}\)
\(m_1 = \dfrac{6\:-\:7}{6 \:-\:2}\)
\(m_1 = -\dfrac{1}{4}\)
Mencari gradien garis singgung lingkaran \((m_2)\)
Garis AB dan garis singgung lingkaran saling tegak lurus, maka berlaku \(m_1 \cdot m_2 = -1\)
\(-\dfrac{1}{4} \cdot m_2 = -1\)
\(m_2 = 4\)
Menentukan pusat dan jari-jari lingkaran \(x^2 + y^2 \:-\:12x + 4y + 23 =0\)
Pusat = \((6, -2)\)
Jari-jari = \(\sqrt{6^2 + (-2)^2\:-\:23}\)
Jari-jari = \(\sqrt{17}\)
Menentukan persamaan garis singgung pada lingkaran yang berpusat di \((6, -2)\), berjari-jari \(\sqrt{17}\) dan bergradien 4
\(\color{blue} y\:-\:b = m(x\:-\:a) \pm r\sqrt{1 + m^2}\)
\(y + 2 = 4(x\:-\:6) \pm \sqrt{17} \sqrt{1 + 4^2}\)
\(y + 2 = 4x\:-\:24 \pm 17\)
\(y = 4x \:-\:26 \pm 17\)
Persamaan garis singgung pertama: \(y = 4x \:-\:9\)
Persamaan garis singgung pertama: \(y = 4x \:-\:43\)
Soal 03
Tempat kedudukan titik-titik yang mempunyai kuasa sama terhadap lingkaran \(\text{L}_1 : x^2 + y^2 + 2x\:-\:4y \:-\:6 = 0\) dan \(\text{L}_2 : x^2 + y^2 \:-\:7x + 5y \:-\:24 = 0\) adalah \(y = mx + c\), nilai dari \(m + c = \dotso\)
(A) 1
(B) 2
(C) 3
(D) 4
(E) 5
Answer: C
Persamaan garis kuasa \(\text{L}_1 \:-\:\text{L}_2 = 0\)
\(x^2 + y^2 + 2x\:-\:4y \:-\:6 \:-\:(x^2 + y^2 \:-\:7x + 5y \:-\:24) = 0\)
\(9x\:-\:9y + 18 = 0\)
\(x\:-\:y + 2 = 0\)
\(y = x + 2\)
\(\color{blue} y = mx + c\)
\(m = 1\) dan \(c = 2\)
\(m + c = 3\)
Soal 04
Garis kuasa lingkaran \(\text{L}_1 : x^2 + y^2 \:-\:13x \:-\:17 = 0\) dan lingkaran \(\text{L}_2 : x^2 + y^2 \:-\:6x + 14y + 11 = 0\) adalah \(x + ay + b = 0\). Garis kuasa ini akan memotong sumbu X di titik \(\text{A}(m, 0)\). Nilai dari \(a + b + m = \dotso\)
(A) 1
(B) 2
(C) 3
(D) 4
(E) 5
Answer: B
Persamaan garis kuasa \(\text{L}_1 \:-\:\text{L}_2 = 0\)
\(x^2 + y^2 \:-\:13x \:-\:17 \:-\:(x^2 + y^2 \:-\:6x + 14y + 11) = 0\)
\(-7x \:-\:14y \:-\:28 = 0\)
\(x + 2y + 4 = 0\)
\(\color{blue} x + ay + b = 0\)
\(a = 2\)
\(b = 4\)
Garis \(x + 2y + 4 = 0\) memotong sumbu X jika \(y = 0\)
\(x + 2(0) + 4 = 0\)
\(x = -4\)
\(m = -4\)
Jadi \(a + b + m = 2 + 4 \:-\:4 = 2\)
Soal 05
Pada gambar di bawah ini, titik \(\text{A}(13, 9)\) di luar lingkaran \(\text{L} : (x + 2)^2 + (y\:-\:1)^2 = 33\), serta ketiga titik B, M, N terletak pada lingkaran. Jika AB garis singgung lingkaran dan AM = 12,5, maka AB − MN = …
(A) 7
(B) 7,96
(C) 7,98
(D) 8
(E) 8,02
Answer: E
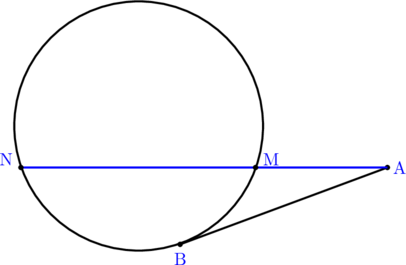
Langkah 1: Menentukan panjang garis singgung AB
\(\text{AB} = \sqrt{K}\)
\(\text{AB} = \sqrt{(x+2)^2 + (y\:-\:1)^2\:-\:33}\)
Substitusi titik A(13, 9)
\(\text{AB} = \sqrt{(13+2)^2 + (9\:-\:1)^2\:-\:33}\)
\(\text{AB} = \sqrt{225 + 64\:-\:33}\)
\(\text{AB} = \sqrt{256}\)
\(\text{AB} = 16\)
Langkah 2: Menentukan panjang MN
\(\text{AB}^2 = \text{AM} \cdot \text{AN}\)
\(16^2 = 12,5 \cdot \text{AN}\)
\(\text{AN} = \dfrac{256}{12,5} = 20,48\)
\(\text{MN} = \text{AN} \:-\: \text{AM}\)
\(\text{MN} = 20,48 \:-\:12,5 = 7,98\)
Jadi \(\text{AB} \:-\: \text{MN} = 16\:-\:7,98 = 8,02\)
Soal 06
Pada gambar di bawah ini, titik A dan B terletak pada lingkaran \(\text{L} : x^2 + y^2 \:-\:11x \:-\:13y \:-\:17=0\). Jika titik \(\text{Q}(7, 4)\) terletak di dalam lingkaran \(\text{L}\) dan \(\text{AQ} = 6\) maka panjang \(\text{BQ} = \dotso\)
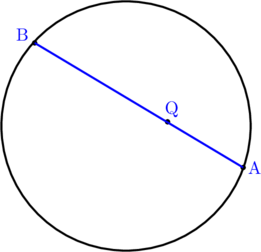
(A) 8
(B) 9
(C) \(\dfrac{27}{2}\)
(D) \(\dfrac{32}{2}\)
(E) \(\dfrac{49}{2}\)
Answer: C
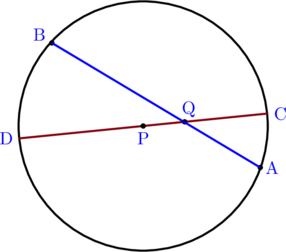
\(\text{L} : x^2 + y^2 \:-\:11x \:-\:13y \:-\:17=0\)
\(\text{P}\left(-\dfrac{1}{2}A, -\dfrac{1}{2}B \right) = \text{P}\left(\dfrac{11}{2}, \dfrac{13}{2} \right)\)
\(\text{r} = \sqrt{\left(\dfrac{11}{2}\right)^2 + \left(\dfrac{13}{2}\right)^2 \:-\:(-17)}\)
\(\text{r} = \sqrt{\left(\dfrac{121}{4}\right) + \left(\dfrac{169}{4}\right) + 17}\)
\(\text{r} = \sqrt{\dfrac{179}{2}}\)
Jarak titik P ke Q
\(\text{PQ} = \sqrt{\left(\dfrac{11}{2}\:-\:7\right)^2 + \left(\dfrac{13}{2}\:-\:4 \right)^2}\)
\(\text{PQ} = \sqrt{\left(\dfrac{9}{4}\right) + \left(\dfrac{25}{4} \right)}\)
\(\text{PQ} = \sqrt{\dfrac{34}{4}} = \dfrac{1}{2}\sqrt{34}\)
Jarak titik C ke Q
\(\text{CQ} = \text{r} \:-\:\text{PQ}\)
\(\text{CQ} = \sqrt{\dfrac{179}{2}}\:-\:\dfrac{1}{2}\sqrt{34}\)
Jarak titik Q ke D
\(\text{QD} = \text{ diameter} \:-\: \text{CQ}\)
\(\text{QD} = 2 \sqrt{\dfrac{179}{2}} \:-\:(\dfrac{179}{2} \:-\:\dfrac{1}{2}\sqrt{34})\)
\(\text{QD} = \sqrt{\dfrac{179}{2}} + \dfrac{1}{2}\sqrt{34}\)
Perbandingan ruas garis yang berpotongan di dalam lingkaran:
\(\color{blue} \text{AQ}\cdot \text{QB} = \text{CQ} \cdot \text{QD}\)
\(6\cdot \text{QB} = \left(\sqrt{\dfrac{179}{2}} \:-\:\dfrac{1}{2}\sqrt{34}\right) \cdot \left(\sqrt{\dfrac{179}{2}} + \dfrac{1}{2}\sqrt{34}\right)\)
\(6\cdot \text{QB} = \left(\sqrt{\dfrac{179}{2}} \:-\:\dfrac{1}{2}\sqrt{34}\right) \cdot \left(\sqrt{\dfrac{179}{2}} + \dfrac{1}{2}\sqrt{34}\right)\)
\(6\cdot \text{QB} = \dfrac{179}{2} \:-\: \dfrac{34}{4}\)
\(6\cdot \text{QB} = \dfrac{358}{4} \:-\: \dfrac{34}{4}\)
\(6\cdot \text{QB} = \dfrac{324}{4}\)
\(\text{QB} = \dfrac{324}{24}\)
\(\text{QB} = \dfrac{27}{2}\)
Soal 07
Persamaan garis singgung lingkaran \(x^2 + y^2 + 4x \:-\:6y + 4 = 0\) yang tegak lurus dengan persamaan garis singgung lingkaran \(x^2 + y^2 = 100\) di titik (6, 8) adalah…
(A) \(y_1 = \dfrac{4}{5}x + \dfrac{32}{3}\) dan \(y_2= \dfrac{4}{5}x + \dfrac{2}{3}\)
(B) \(y_1 = \dfrac{1}{3}x + \dfrac{32}{3}\) dan \(y_2= \dfrac{1}{3}x + \dfrac{2}{3}\)
(C) \(y_1 = \dfrac{1}{3}x + \dfrac{32}{3}\) dan \(y_2= \dfrac{4}{3}x + \dfrac{2}{3}\)
(D) \(y_1 = \dfrac{2}{3}x + \dfrac{32}{3}\) dan \(y_2= \dfrac{4}{3}x + \dfrac{2}{3}\)
(E) \(y_1 = \dfrac{4}{3}x + \dfrac{32}{3}\) dan \(y_2= \dfrac{4}{3}x + \dfrac{2}{3}\)
Answer: E
Persamaan garis singgung lingkaran \(x^2 + y^2 = 100\) di titik (6, 8) adalah sebagai berikut:
\(x_1 \cdot x + y_1 \cdot y = 100\)
\(6x + 8y = 100\)
Bagi kedua ruas dengan 2
\(3x + 4y = 50\)
\(4y = -3x + 50\)
\(y = -\dfrac{3}{4}x + \dfrac{50}{4}\)
Gradien \(m_1 = -\dfrac{3}{4}\)
Misal gradien garis singgung lingkaran \(x^2 + y^2 + 4x \:-\:6y + 4 = 0\) adalah \(m_2\)
Gunakan syarat dua garis saling tegak lurus \(m_1 \cdot m_2 = -1\)
\(-\dfrac{3}{4} \cdot m_2 = -1\)
\(m_2 = \dfrac{4}{3}\)
Lingkaran \(x^2 + y^2 + 4x \:-\:6y + 4 = 0\) berpusat di titik (-2, 3) dengan jari-jari 3
Persamaan garis singgung pada lingkaran yang berpusat di titik (-2, 3) dengan jari-jari 3 dan bergradien \(m_2 = \dfrac{4}{3}\) adalah:
\(y\:-\:b = m(x\:-\:a) \pm r\sqrt{1 + m^2}\)
\(y\:-\:3 = \dfrac{4}{3}(x + 2) \pm 3\sqrt{1 + \dfrac{16}{9}}\)
\(y\:-\:3 = \dfrac{4}{3}(x + 2) \pm 3\cdot \dfrac{5}{3}\)
\(y = \dfrac{4}{3}x + \dfrac{8}{3} + 3 \pm 5\)
Persamaan garis singgung yang pertama:
\(y_1 = \dfrac{4}{3}x + \dfrac{8}{3} + 3 + 5\)
\(y_1 = \dfrac{4}{3}x + \dfrac{32}{3}\)
Persamaan garis singgung yang kedua:
\(y_2 = \dfrac{4}{3}x + \dfrac{8}{3} + 3 \:-\:5\)
\(y_2= \dfrac{4}{3}x + \dfrac{2}{3}\)
Soal 08
Pada gambar di bawah ini, persamaan lingkaran pertama \(\text{L}_1 \equiv x^2 + y^2 \:-\:14x\:-\:8y + 49 = 0\), dan persamaan lingkaran kedua \(\text{L}_2 \equiv x^2 + y^2 \:-\:38x \:-\:18y + 361 = 0\).

Persamaan lingkaran yang ketiga adalah…
(A) \((x\:-\:10,8)^2 + (y\:-\:1,44)^2 = (1,24)^2\)
(B) \((x\:-\:11,8)^2 + (y\:-\:1,44)^2 = (1,44)^2\)
(C) \((x\:-\:12,8)^2 + (y\:-\:1,44)^2 = (1,64)^2\)
(D) \((x\:-\:13,8)^2 + (y\:-\:1,44)^2 = (1,84)^2\)
(E) \((x\:-\:14,8)^2 + (y\:-\:1,44)^2 = (1,84)^2\)
Answer: B
Menentukan pusat dan jari-jari lingkaran 1
\(\text{L}_1 \equiv x^2 + y^2 \:-\:14x\:-\:8y + 49 = 0\)
\(\text{P}(-\frac{1}{2}(-14), -\frac{1}{2}(-8))\)
\(\text{P}(7, 4)\)
\(\text{R}_1 = \sqrt{7^2 + 4^2 \:-\:49}\)
\(\text{R}_1 = 4\)
Menentukan pusat dan jari-jari lingkaran 2
\(\text{L}_2 \equiv x^2 + y^2 \:-\:38x \:-\:18y + 361 = 0\)
\(\text{P}(-\frac{1}{2}(-38), -\frac{1}{2}(-18))\)
\(\text{P}(19, 9)\)
\(\text{R}_2 = \sqrt{19^2 + 9^2 \:-\:361}\)
\(\text{R}_2 = \sqrt{81}\)
\(\text{R}_2 = 9\)
Menentukan jari-jari dan pusat lingkaran ke-3
Misal pusat lingkaran ke-3 adalah \((a, b)\) dan jari-jarinya \(b\).
\(b = \dfrac{\text{R}_1 \times \text{R}_2}{\left(\sqrt{\text{R}_1} + \sqrt{\text{R}_2}\right)^2}\)
\(b = \dfrac{4 \times 9}{\left(\sqrt{4} + \sqrt{9}\right)^2}\)
\(b = \dfrac{36}{25} = 1,44\)
Buat segitiga siku-siku dengan sisi miringnya adalah jarak antara pusat lingkaran 1 dan lingkaran 3.
Gunakan rumus pythagoras untuk menentukan \(a\)
\((a\:-\:7)^2 + (4\:-\:b)^2 = (4 + b)^2\)
\((2,56)^2 + (a\:-\:7)^2 = (5,44)^2\)
\(6,5536 + (a\:-\:7)^2 = 29,5936\)
\((a\:-\:7)^2 = 23,04\)
\(a\:-\:7 = \pm \sqrt{23,04}\)
\(a\:-\:7 = + 4,8\)
\(a = 11,8\)
Menentukan persamaan lingkaran ke-3
Persamaan lingkaran berpusat di \((11.8, 1.44)\) dan berjari-jari 1,44 adalah:
\((x\:-\:11,8)^2 + (y\:-\:1,44)^2 = (1,44)^2\)
