Penyelesaian yang melibatkan nilai mutlak:
(1) Jika \(a\) bilangan real positif, maka:
- \(|x| \leq a \Leftrightarrow -a \leq x \leq a\)
- \(|x| \geq a \Leftrightarrow x \geq a \text{ atau } x \leq -a\)
(2) Dengan menggunakan definisi nilai mutlak
\(|x|=\begin{cases}x & x \geq 0\\-x & x < 0\end{cases}\)
Contoh Soal
Tentukan solusi pertidaksamaan \(|x \:-\: 5| > 3\)
Cara I:
\(|x \:-\:5| > 3\)
\(x \:-\: 5 > 3 \text{ atau } x \:-\: 5 < -3\)
\(x > 3 + 5 \text{ atau } x < -3 + 5\)
\(x > 8 \text{ atau } x < 2\)
Solusi pertidaksamaan \(|x \:-\: 5| > 3\) adalah \(x < 2 \text{ atau } x > 8\)
Cara II:
\(|x \:-\: 5| > 3\)
\(\color{blue}\text{kuadratkan kedua ruas}\)
Note: cara kuadratkan kedua ruas ini hanya dilakukan saat kedua ruas nilainya sudah pasti positif ya teman
\((x \:-\: 5)^2 > 3^2\)
\((x \:-\: 5)^2 \:-\:3^2 > 0\)
\(\color{blue}a^2 \:-\: b^2 = (a + b)(a \:-\:b)\)
\((x\:-\: 5 + 3)(x\:-\: 5\:-\: 3) > 0\)
\((x \:-\: 2)(x \:-\: 8) > 0\)
\(\text{Pembuat nol:}\)
\(x \:-\:2 = 0 \rightarrow x = 2\)
\(x \:-\:8 = 0 \rightarrow x = 8\)

Solusi pertidaksamaan \(|x\:-\: 5| > 3\) adalah daerah yang bertanda positif, yaitu \(x < 2, \text{ atau } x > 8\)
Tentukan solusi pertidaksamaan \(|2x\:-\: 3| \leq 7\)
\(|2x \:-\: 3| \leq 7\)
\(-7 \leq 2x \:-\: 3 \leq 7\)
\(-7 + 3 \leq 2x \leq 7 + 3\)
\(-4 \leq 2x \leq 10\)
\(-\dfrac{4}{2} \leq x \leq \dfrac{10}{2}\)
\(-2 \leq x \leq 5\)
Jadi solusi pertidaksamaan \(|2x \:-\: 3| \leq 7\) adalah \(-2 \leq x \leq 5\)
Tentukan solusi pertidaksamaan \(|x \:-\: 4| > 1\:-\:2x\)
Dengan menggunakan definisi nilai mutlak,
\(|x\:-\:4|=\begin{cases}+(x\:-\:4) & x \geq 4\\-(x\:-\:4) & x < 4\end{cases}\)
| \(x < 4 \) | \(x \geq 4\) |
| \(-(x \:-\: 4) > 1\:-\:2x\)
\(-x + 4 > 1 \:-\:2x\) \(-x + 2x > 1 \:-\: 4\) \(x > – 3\) |
\(x \:-\: 4 > 1\:-\:2x\)
\(x + 2x > 1 + 4\) \(3x > 5\) \(x > \dfrac{5}{3}\) |
| Selanjutnya, tentukan irisan dari \(x > – 3\) dan \(x < 4 \)
Solusi: \(-3 < x < 4\) |
Selanjutnya, tentukan irisan dari \(x > \dfrac{5}{3}\) dan \(x \geq 4\)
Solusi: \(x \geq 4\) |
Penyelesaian pertidaksamaan \(|x \:-\: 4| > 1\:-\:2x\) adalah gabungan dari solusi bagian kiri dan solusi bagian kanan
Solusi akhir: \(x > -3\)
Tentukan solusi pertidaksamaan \(\left|\dfrac{2x\:-\:3}{x + 1}\right| \geq 1\)
\(\left|\dfrac{2x\:-\:3}{x + 1}\right| \geq 1\)
\(\dfrac{2x\:-\:3}{x +1} \geq 1 \text{ atau } \dfrac{2x \:-\:3}{x + 1} \leq -1\)
Kemungkinan 1:
\(\dfrac{2x\:-\:3}{x +1} \geq 1\)
\(\dfrac{2x\:-\:3}{x +1} \:-\:1 \geq 0\:\:\:\:\:\color{blue}\text{samakan penyebut}\)
\(\dfrac{2x\:-\:3\:-\:(x + 1)}{x +1} \geq 0\)
\(\dfrac{2x\:-\:3\:-\:x\:-\: 1}{x +1} \geq 0\)
\(\dfrac{x \:-\:4}{x +1} \geq 0\)
\(\text{Pembuat nol:}\)
\(x \:-\: 4 = 0 \rightarrow x = 4\)
\(x + 1 \neq 0 \rightarrow x \neq -1\)

Solusi pertidaksamaan \(\left|\dfrac{2x\:-\:3}{x + 1}\right| \geq 1\) adalah \(x < -1 \text{ atau } x \geq 4\)
Kemungkinan 2:
\(\dfrac{2x \:-\:3}{x + 1} \leq -1\)
\(\dfrac{2x\:-\: 3}{x + 1} + 1 \leq 0\:\:\:\:\:\color{blue}\text{samakan penyebut}\)
\(\dfrac{2x\:-\:3 + (x + 1)}{x + 1}\leq 0\)
\(\dfrac{2x \:-\:3 + x + 1}{x + 1}\leq 0\)
\(\dfrac{3x \:-\:2}{x + 1}\leq 0\)
\(\text{Pembuat nol:}\)
\(3x\:-\: 2 = 0 \rightarrow x = \dfrac{2}{3}\)
\(x + 1 \neq 0 \rightarrow x \neq -1\)
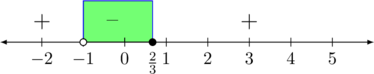
Solusi pertidaksamaan \(\dfrac{2x\:-\: 3}{x + 1} \leq -1\) adalah \(x < -1 \text{ atau } x \geq \frac{2}{3}\)
Solusi akhir adalah gabungan dari solusi 1 dan solusi 2, yaitu:
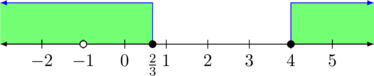
\(x \leq \frac{2}{3} \text{ atau } x \geq 4, \: x \neq -1\)
Tentukan solusi pertidaksamaan \(|x \:-\: 4|^2 \:-\: 7|x \:-\: 4| + 10 \leq 0\)
\(|x \:-\: 4|^2 \:-\: 7|x\:-\: 4| + 10 \leq 0\)
\(\text{Misal } |x \:-\: 4| = p\)
\(p^2\:-\:7p + 10 \leq 0\)
\((p \:-\:5)(p \:-\: 2) \leq 0\)
\(\text{Pembuat nol:}\)
\(p\:-\: 5 = 0 \rightarrow p = 5\)
\(p \:-\: 2 = 0 \rightarrow p = 2\)

\(2 \leq p \leq 5\)
\(2 \leq |x \:-\: 4| \leq 5\)
\(|x \:-\: 4| \geq 2 \text{ dan } |x \:-\:4| \leq 5\)
\(\text{Kemungkinan 1: } |x \:-\: 4| \geq 2\)
\(x \:-\: 4 \geq 2 \text{ atau } x\:-\: 4 \leq -2\)
\(x \geq 2 + 4 \text{ atau } x \leq -2 + 4\)
\(\text{Solusi 1: } x \geq 6 \text{ atau } x \leq 2\)
\(\text{Kemungkinan 2: } |x \:-\: 4| \leq 5\)
\(-5 \leq x \:-\: 4 \leq 5\)
\(-5 + 4 \leq x \leq 5 + 4\)
\(\text{Solusi 2: } -1 \leq x \leq 9\)
Solusi akhir adalah irisan dari solusi 1 dan solusi 2, yaitu:

\(-1 \leq x \leq 2 \text{ atau } 6 \leq x \leq 9\)
Tentukan solusi pertidaksamaan \(|x \:-\: 1| + |x \:-\: 2| \leq 5\)
Dengan menggunakan definisi nilai mutlak,
\(|x\:-\:1|=\begin{cases}+(x\:-\:1) & x \geq 1\\-(x\:-\:1) & x < 1\end{cases}\)
\(|x\:-\:2|=\begin{cases}+(x\:-\:2) & x \geq 2\\-(x\:-\: 2) & x < 2\end{cases}\)
| \(x < 1\) | \(1 \leq x < 2\) | \( x \geq 2\) |
| \(-(x \:-\: 1) \:-\:(x \:-\: 2) \leq 5\)
\(-x + 1 \:-\:x + 2 \leq 5\) \(-2x + 3 \leq 5\) \(-2x \leq 5 – 3\) \(-2x \leq 2\:\:\:\:\:\color{blue}\text{bagi kedua ruas dengan } – 2\) \(x \geq -1\) |
\((x\:-\: 1)\:-\:(x \:-\: 2) \leq 5\)
\(x \:-\: 1 \:-\: x + 2 \leq 5\) \(1\leq 5\) Pernyataan yang bernilai benar
|
\((x \:-\:1) + (x \:-\: 2) \leq 5\)
\(2x \:-\: 3\leq 5\) \(2x \leq 5 + 3\) \(2x \leq 8\:\:\:\:\:\color{blue}\text{bagi kedua ruas dengan } 2\) \(x \leq 4\) |
| Selanjutnya, tentukan irisan dari \(x \geq -1\) dan \(x < 1\)
Solusi: \(-1 \leq x < 1\) |
Solusi: \(1 \leq x < 2\) | Selanjutnya, tentukan irisan dari \(x \leq 4\) dan \( x \geq 2\)
Solusi: \(2 \leq x \leq 4\) |
Solusi akhir adalah gabungan dari solusi 1, solusi 2, dan solusi 3, yaitu \(-1 \leq x \leq 4\)

Tentukan solusi dari pertidaksamaan \(|x + 2| + |x \:-\: 3| > x + 5\)
Dengan menggunakan definisi nilai mutlak,
\(|x+2|=\begin{cases}+(x+2) & x \geq -2\\-(x+2) & x < -2\end{cases}\)
\(|x\:-\:3|=\begin{cases}+(x\:-\:3) & x \geq 3\\-(x\:-\: 3) & x < 3\end{cases}\)
| \(x < -2\) | \(-2 \leq x < 3\) | \( x \geq 3\) |
| \(-(x + 2)\:-\:(x \:-\: 3) > x + 5\)
\(-x \:-\: 2 \:-\: x + 3 > x + 5\) \(-2x + 1 > x + 5\) \(-2x – x > 5 \:-\: 1\) \(-3x > 4\) \(x < -\dfrac{4}{3}\) |
\(x + 2 \:-\:(x \:-\: 3) > x + 5\)
\(x + 2\:-\: x + 3 > x + 5\) \(5 > x + 5\) \(x < 0\)
|
\(x + 2 + x \:-\: 3 > x + 5\)
\(2x \:-\:1 > x + 5\) \(2x \:-\:x > 5 + 1\) \(x > 6\)
|
| Selanjutnya, tentukan irisan dari \(x < -\dfrac{4}{3}\) dan \(x < -2\)
Solusi: \(x < -2\) |
Selanjutnya, tentukan irisan dari \(x < 0\) dan \(-2 \leq x < 3\)
Solusi: \(-2 \leq x < 0\) |
Selanjutnya, tentukan irisan dari \(x > 6\) dan \( x \geq 3\)
Solusi: \(x > 6\) |
Solusi akhir adalah gabungan dari solusi 1, solusi 2, dan solusi 3, yaitu \(x < 0 \text{ atau } x > 6\)

Tentukan solusi dari pertidaksamaan \(|x^2 + 2x \:-\: 3| \geq |x \:-\: 1|\)
\(|x^2 + 2x \:-\:3| \geq |x \:-\:1|\)
\(\color{blue}\text{kuadratkan kedua ruas}\)
\((x^2 + 2x \:-\: 3)^2 \geq (x \:-\: 1)^2\)
\((x^2 + 2x \:-\: 3)^2\:-\: (x \:-\: 1)^2 \geq 0\)
\(\color{blue}a^2 – b^2 = (a + b)(a \:-\: b)\)
\((x^2 + 2x\:-\: 3 + x \:-\: 1)(x^2 + 2x \:-\:3 \:-\:(x \:-\:1))\geq 0\)
\((x^2 + 3x \:-\: 4)(x^2 + x\:-\:2) \geq 0\)
\((x + 4)(x\:-\: 1)(x + 2)(x \:-\: 1) \geq 0\)
\((x + 4)(x + 2)(x \:-\: 1)^2 \geq 0\)
\(\text{Pembuat nol:}\)
\(x + 4 = 0 \rightarrow x = -4\)
\(x + 2 = 0 \rightarrow x = -2\)
\(x \:-\: 1 = 0 \rightarrow x = 1\)

Solusi pertidaksamaannya adalah \(x \leq -4 \text{ atau } x \geq -2\)
