BENTUK 1
\(\color{blue} \sqrt{f(x)} \geq p, \text{ dengan } p > 0\)
Langkah penyelesaian:
- Syarat terdefinisi bentuk akar, \(f(x) \geq 0\)
- Kuadratkan kedua ruas
- Tentukan irisan dari penyelesaian 1 dan 2
Contoh 1
\(\sqrt{x \:-\: 5}\geq 1\)
Langkah 1: Syarat terdefinisi bentuk akar
\(x\: -\: 5 \geq 0\)
\(x \geq 5\)
Langkah 2: Kuadratkan kedua ruas
\(\left(\sqrt{x \:-\:5}\right)^2 \geq 1^2\)
\(x\: -\: 5 \geq 1\)
\(x \geq 6\)
Langkah 3: Tentukan irisan penyelesaian 1 dan 2

Irisannya adalah \(x \geq 6\)
Contoh 2
\(\sqrt{2x+4}< 4\)
Langkah 1: Syarat terdefinisi bentuk akar
\(2x + 4 \geq 0\)
\(2x \geq -4\)
\(x \geq \dfrac{-4}{2}\)
\(x \geq -2\)
Langkah 2: Kuadratkan kedua ruas
\(\left(\sqrt{2x + 4}\right)^2 < 4^2\)
\(2x + 4 < 16\)
\(2x < 12\)
\(x < \dfrac{12}{2}\)
\(x < 6\)
Langkah 3: Tentukan irisan penyelesaian 1 dan 2

Irisannya adalah \(-2\leq x < 6\)
Contoh 3
\(\sqrt{x^2 + 5x + 6} < \sqrt{2}\)
Langkah 1: Syarat terdefinisi bentuk akar
\(x^2 + 5x + 6 \geq 0\)
\((x + 3)(x + 2) \geq 0\)
\(\text{Pembuat nol:}\)
\(x + 3 = 0 \rightarrow x = -3\)
\(x + 2 = 0 \rightarrow x = -2\)
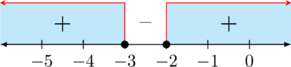
Solusi 1: \(x \leq -3 \text{ atau } x \geq -2\)
Langkah 2: Kuadratkan kedua ruas
\(\left(\sqrt{x^2 + 5x + 6}\right)^2 < (\sqrt{2})^2\)
\(x^2 + 5x + 6 < 2\)
\(x^2 + 5x + 6 – 2 < 0\)
\((x^2 + 5x + 4) < 0\)
\((x + 4)(x +1) < 0\)
Pembuat nol:
\(x + 4 = 0 \rightarrow x = -4\)
\(x + 1 = 0 \rightarrow x = -1\)

Solusi 2: \(-4<x < -1\)
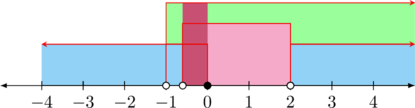
Langkah 3: Tentukan irisan penyelesaian 1 dan 2
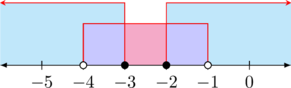
Irisannya adalah \(-4<x\leq -3 \text{ atau } -2\leq x < -1\)
Bentuk 2
\(\color{blue} \sqrt{f(x)} < p, \text{ dengan } p < 0\)
Tidak ada nilai \(x \in \Re\) yang memenuhi
Contoh
\(\sqrt{2x + 16} < -1\)
Tidak ada nilai \(\color{red} x \in \Re\) yang memenuhi
BENTUK 3
\(\color{blue} \sqrt{f(x)} > p, \text{ dengan } p < 0\)
Solusi: \(f(x) \geq 0\)
\(\sqrt{x^2\:-\:9} > -1\)
\(x^2\:-\:9\geq 0\)
\(x^2\:-\:3^2\geq 0\:\:\:\:\:\color{blue} a^2\: - \:b^2 = (a + b)(a\: -\: b)\)
\((x + 3)(x\: - \:3) \geq 0\)
Pembuat nol:
\(x + 3 = 0 \rightarrow x = -3\)
\(x \:- \:3 = 0 \rightarrow x = 3\)

Jadi solusinya adalah \(x \leq -3 \text{ atau } x \geq 3\)
BENTUK 4
\(\color{blue} \sqrt{f(x)} > \sqrt{g(x)}\)
Langkah penyelesaian:
- Syarat terdefinisi bentuk akar: \(f(x) \geq 0 \text{ dan } g(x) \geq 0\)
- Kuadratkan kedua ruas
- Tentukan irisan dari penyelesaian 1 dan 2
Contoh 1
\(\sqrt{x + 5} > \sqrt{x \:-\: 1}\)
Langkah 1: Syarat terdefinisi bentuk akar
\(f(x) \geq 0 \text{ dan } g(x) \geq 0\)
\(x + 5 \geq 0\text{ dan } x - 1 \geq 0\)
\(x \geq -5 \text { dan } x \geq 1\:\:\:\:\:\color{blue}\text{irisan}\)
Solusi 1: \(x \geq 1\)
Langkah 2: Kuadratkan kedua ruas
\(\left(\sqrt{x + 5}\right)^2 > \left(\sqrt{x \:- \:1}\right)^2\)
\(\cancel{x} + 5 > \cancel{x}\:- \:1\)
Solusi 2: \(x \in \Re\)
Langkah 3: Tentukan irisan penyelesaian 1 dan 2
Irisan dari \(x \geq 1\) dan \(x \in \Re\) adalah \(\color{purple} x \geq 1\)
Contoh 2
\(\sqrt{x^2 + 8x + 12} > \sqrt{2x + 3 }\)
Langkah 1: Syarat terdefinisi bentuk akar
\(\color{red} f(x) \geq 0\)
\(x^2 + 8x + 12 \geq 0\)
\((x + 6)(x + 2) \geq 0\)
Pembuat nol:
\(x + 6 = 0 \rightarrow x = -6\)
\(x + 2 = 0 \rightarrow x = -2\)
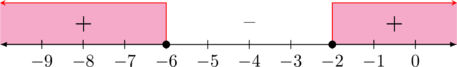
\(\color{red} x \leq -6 \text{ atau } x \geq -2\)
\(\color{blue} g(x) \geq 0\)
\(2x + 3\geq 0\)
\(2x \geq -3\)
\(\color{blue} x \geq -\dfrac{3}{2}\)
Irisan dari \(x \leq -6 \text{ atau } x \geq -2\) dan \(x \geq -\dfrac{3}{2}\) adalah \(\color{purple} x \geq -\dfrac{3}{2}\)
Langkah 2: Kuadratkan kedua ruas
\(\left(\sqrt{x^2 + 8x + 12}\right)^2 > \left(\sqrt{2x + 3}\right)^2\)
\(x^2 + 8x + 12 > 2x + 3\)
\(x^2 + 8x \:-\:2x + 12 \:-\: 3 > 0\)
\(x^2 + 6x + 9> 0\)
\((x + 3)^2 > 0\)
Solusi 2: berlaku untuk semua \(x \in \Re\)
Langkah 3: Tentukan irisan penyelesaian 1 dan 2
Irisan dari \(x \geq -\dfrac{3}{2}\) dan \(x \in \Re\) adalah \(\color{purple} x \geq -\dfrac{3}{2}\)
Contoh 3
\(\sqrt{x^2 + x \:-\: 12} < \sqrt{x^2 + 4x \:-\: 12 }\)
Langkah 1: Syarat terdefinisi bentuk akar
\(\color{red} f(x) \geq 0\)
\(x^2 + x \:-\: 12 \geq 0\)
\((x + 4)(x \:-\:3) \geq 0\)
Pembuat nol:
\(x + 4 = 0 \rightarrow x = -4\)
\(x\: -\:3 = 0 \rightarrow x = 3\)
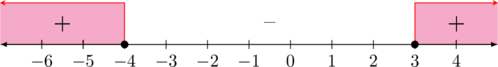
\(\color{blue} g(x) \geq 0\)
\(x^2 + 4x \:- \:12\geq 0\)
\((x + 6)(x\: - \:2) \geq 0\)
Pembuat nol:
\(x + 6 = 0 \rightarrow x = -6\)
\(x \:-\:2 = 0 \rightarrow x = 2\)
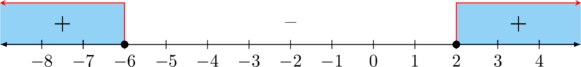
Irisan dari kedua syarat terdefinisi di atas adalah: \(\color{purple}x \leq - 6 \text{ atau } x \geq 3\)
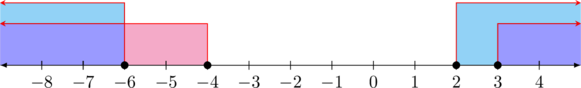
Langkah 2: Kuadratkan kedua ruas
\(\left(\sqrt{x^2 + x \: - \:12}\right)^2 < \left(\sqrt{x^2 + 4x \:- \:12}\right)^2\)
\(x^2 + x \:- \:12 < x^2 + 4x\: - \:12\)
\(x \:- \:4x < 0\)
\(-3x < 0\:\:\:\:\:\color{blue}\text{bagi kedua ruas dengan } - 3\)
Note: jika kedua ruas dikali atau dibagi angka negatif maka tanda pertidaksamaan berubah
\(x > 0\)
Solusi 2: \(\color{purple} x > 0\)
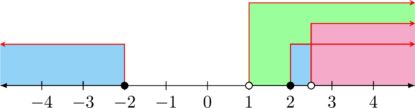
Langkah 3: Tentukan irisan penyelesaian 1 dan 2
Irisan dari \(\color{purple}x \leq - 6 \text{ atau } x \geq 3\) dan \(\color{purple} x > 0\), adalah \(x \geq 3\)
BENTUK 5
\(\color{blue} \sqrt{f(x)} > g(x)\)
Langkah penyelesaian:
| Kemungkinan 1: (+)(+) | Kemungkinan 2: (+)(-) |
| 1. Syarat terdefinisi bentuk akar, \(f(x) \geq 0\)
2. \(g(x) > 0\) 3. Kuadratkan kedua ruas Iris penyelesaian 1, 2, dan 3 |
1. Syarat terdefinisi bentuk akar, \(f(x) \geq 0\)
2. \(g(x) < 0\) Iris penyelesaian 1 dan 2 |
|
Solusi akhir adalah gabungan dari solusi kemungkinan 1 dan solusi kemungkinan 2 |
|
Contoh 1
\(\sqrt{x^2 \:- \:4} > x \:-\: 1\)
| Kemungkinan 1: (+)(+) | Kemungkinan 2: (+)(-) |
| Langkah 1: Syarat terdefinisi bentuk akar
\(x^2\: - \:4 \geq 0\) \((x + 2)(x\: - \:2) \geq 0\) \(\color{blue} x \leq -2 \text{ atau } x \geq 2\)
Langkah 2: \(g(x) > 0\) \(x \:- \:1 > 0\) \(\color{green} x > 1\)
Langkah 3: Kuadratkan kedua ruas \(\left(\sqrt{x^2\: - \:4}\right)^2 > (x \:- \:1)^2\) \(x^2 \:- \:4 > x^2 \:-\:2x + 1\) \(-5 > -2x\) \(-2x < -5\:\:\:\:\:\color{blue}\text{bagi kedua ruas dengan } -2\) \(\color{magenta} x > \dfrac{5}{2}\)
Irisan dari penyelesaian langkah 1, 2, dan 3 adalah:
\(\color{red} x > \dfrac{5}{2}\) |
Langkah 1: Syarat terdefinisi bentuk akar
\(x^2 \:- \:4 \geq 0\) \((x + 2)(x\: - \:2) \geq 0\) \(\color{blue} x \leq -2 \text{ atau } x \geq 2\)
Langkah 2: \(g(x) < 0\) \(x \:- \:1 < 0\) \(\color{green} x < 1\)
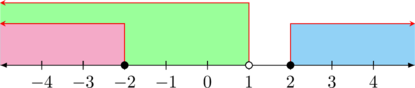
Irisan dari penyelesaian langkah 1 dan 2 adalah:
\(\color{red} x \leq -2\) |
|
Solusi akhir adalah gabungan dari solusi kemungkinan 1 dan solusi kemungkinan 2 \(\color{red} x \leq -2 \text{ atau } x > \dfrac{5}{2}\) |
|
Contoh 2
\(\sqrt{x^2\:-\:2x\:-\:15} > 3\:-\:x\)
| Kemungkinan 1: (+)(+) | Kemungkinan 2: (+)(-) |
| Langkah 1: Syarat terdefinisi bentuk akar
\(x^2\:-\:2x-15\geq 0\) \((x \:-\:5)(x + 3) \geq 0\) \(\color{blue} x \leq -3 \text{ atau } x \geq 5\)
Langkah 2: \(g(x) > 0\) \(3\:-\:x > 0\) \(-x > -3\) \(\color{green} x < 3\)
Langkah 3: Kuadratkan kedua ruas \(\left(\sqrt{x^2\:-\:2x\:-\:15}\right)^2 > (3\:-\:x)^2\) \(x^2\:-\:2x\:-\:15 > 9\: -\: 6x + x^2\) \(4x > 24\) \(\color{magenta} x > 6\)
Tidak ada irisan dari penyelesaian langkah 1, 2, dan 3
\(\color{red} \lbrace \rbrace\) |
Langkah 1: Syarat terdefinisi bentuk akar
\(x^2\:-\:2x-15\geq 0\) \((x\: -\:5)(x + 3) \geq 0\) \(\color{blue} x \leq -3 \text{ atau } x \geq 5\)
Langkah 2: \(g(x) < 0\) \(3\:-\:x < 0\) \(-x < -3\) \(x > 3\) \(\color{green} x > 3\)
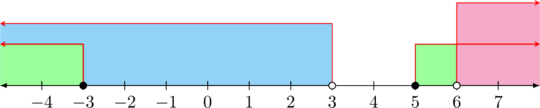
Irisan dari penyelesaian langkah 1 dan 2 adalah:
\(\color{red} x \geq 5\) |
|
Solusi akhir adalah gabungan dari solusi kemungkinan 1 dan solusi kemungkinan 2 \(\color{red} x \geq 5\) |
|
BENTUK 6
\(\color{blue} \sqrt{f(x)} < g(x)\)
Langkah penyelesaian:
- Syarat terdefinisi bentuk akar \(f(x) \geq 0\)
- \(g(x) > 0\)
- Kuadratkan kedua ruas
Contoh 1
\(\sqrt{x + 6} < x + 4\)
Langkah 1: Syarat terdefinisi bentuk akar
\(x + 6 \geq 0\)
\(\color{blue} x \geq -6\)
Langkah 2: \(g(x) > 0\)
\(x + 4 > 0\)
\(\color{green} x > -4\)
Langkah 3: Kuadratkan kedua ruas
\(\left(\sqrt{x + 6}\right)^2 < (x + 4)^2\)
\(x + 6 < x^2 + 8x + 16\)
\(0 < x^2 + 7x + 10\)
\(0 < (x + 5)(x + 2)\)
\(\color{magenta} x < -5 \text{ atau } x > -2 \)
Irisan penyelesaian dari langkah 1, 2, dan 3 adalah: \(x > -2\)
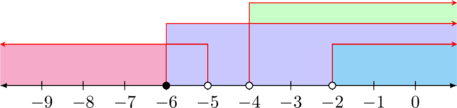
Contoh 2
\(\sqrt{\dfrac{x^3}{x\:-\:2}} < x + 1\)
Langkah 1: Syarat terdefinisi bentuk akar
\(\dfrac{x^3}{x\:-\:2} \geq 0\)

\(\color{blue} x \leq 0 \text{ atau } x > 2\)
Langkah 2: \(g(x) > 0\)
\(x + 1 > 0\)
\(\color{green} x > -1\)
Langkah 3: Kuadratkan kedua ruas
\(\left(\sqrt{\dfrac{x^3}{x\:-\:2}}\right)^2 < (x+1)^2\)
\(\dfrac{x^3}{x\:-\:2}< x^2 + 2x + 1\:\:\:\:\;\color{blue}\text{ samakan penyebut}\)
\(\dfrac{x^3}{x\:-\:2} < \dfrac{(x^2 + 2x + 1)(x \:-\: 2)}{x \:-\: 2}\)
\(\dfrac{x^3}{x\:-\:2} < \dfrac{(x^3\:-\:3x \:-\:2)}{x \:-\: 2}\)
\(\dfrac{x^3}{x\:-\:2} - \dfrac{(x^3 \:-\:3x \:-\:2)}{x\:-\: 2} < 0\)
\(\dfrac{x^3 \:-\: (x^3 \:-\: 3x \:-\:2)}{x\:-\:2}< 0\)
\(\dfrac{3x + 2}{x \:-\: 2} < 0\)

\(\color{magenta} -\dfrac{2}{3} < x < 2 \)
Irisan penyelesaian dari langkah 1, 2, dan 3 adalah: \(\color{purple} -\dfrac{2}{3} < x \leq 0 \)