Bilangan rasional adalah bilangan yang dapat dinyatakan dalam bentuk \(\dfrac{a}{b}\) dengan \(a\) dan \(b\) adalah bilangan bulat, dan \(b\neq 0\).
Contoh bilangan rasional:
- Semua bilangan bulat, \(\dotso, -4, -3, -2, -1, 0, 1, 2, 3, 4, \dotso\) karena bisa ditulis \(\dotso, -\dfrac{2}{1}, -\dfrac{1}{1}, \dfrac{0}{1}, \dfrac{1}{1}, \dfrac{2}{1}, \dotso\)
- Akar yang hasilnya berupa bilangan bulat, atau pecahan desimal. Contoh \(\sqrt{4}, \sqrt[3] {64}, \sqrt{156,25}\)
- Desimal berulang
Cara merubah angka desimal berulang menjadi bentuk pecahan
Contoh 1
\(0,2222222\dotso\)
Misalkan \(x = 0,2222222\dotso\)
Karena ada satu angka yang berulang yaitu 2, maka kalikan 10 kedua ruas
\(10x = 2,2222222\dotso\dotso(1)\)
\(x = 0,2222222\dotso\dotso(2)\)
Kurangkan persamaan (1) dengan persamaan (2)
\(9x = 2\)
\(x = \dfrac{2}{9}\)
Contoh 2
\(2,54545454\dotso\)
Misalkan \(x = 2,54545454\dotso\)
Karena ada dua angka yang berulang yaitu 25, maka kalikan 100 kedua ruas
\(100x = 254,54545454\dotso\dotso(1)\)
\(x = 2,54545454\dotso\dotso(2)\)
Kurangkan persamaan (1) dengan persamaan (2)
\(99x = 252\)
\(x = \dfrac{252}{99}\)
Contoh 3
\(3,125125125125\dotso\)
Misalkan \(x = 3,125125125125\dotso\)
Karena ada tiga angka yang berulang yaitu 125, maka kalikan 1000 kedua ruas
\(1000x = 3125,125125125125\dotso\dotso(1)\)
\(x = 3,125125125125\dotso\dotso(2)\)
Kurangkan persamaan (1) dengan persamaan (2)
\(999x = 3122\)
\(x = \dfrac{3122}{999}\)
Contoh bilangan yang tidak rasional:
- \(\text{Angka desimal tidak berulang}\)
- \(\sqrt{2} = 1,41421356\dotso\)
- \(\pi = 3,14285714\dotso\)
Pertidaksamaan linear
Berikut ini adalah contoh penyelesaian pertidaksamaan linear dalam garis bilangan
(1) \(2x\:-\: 1 > 3\)
\(2x \:-\: 1 > 3\)
\(2x > 3 + 1\)
\(2x > 4\:\:\:\:\:\color{blue}\text{bagi kedua ruas dengan 2}\)
\(x > 2\)
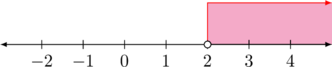
(2) \(5x+2 < 4x+3\)
\(5x+2 < 4x+3\)
\(5x\:-\:4x < 3 \:-\:2\)
\(x < 1\)
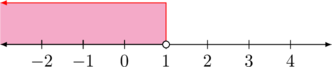
(3) \(7x +3\leq -4 \text{ atau } 3x + 5\geq 8\)
\(7x +3\leq -4\)
\(7x \leq -4 \:-\: 3\)
\(7x \leq -7\)
\(x \leq \dfrac{-7}{7}\)
\(x \leq -1\)
\(\text{atau (gabungan)}\)
\(3x + 5\geq 8\)
\(3x \geq 8 \:-\: 5\)
\(3x \geq 3\)
\(x \geq \dfrac{3}{3}\)
\(x \geq 1\)

Solusi pertidaksamaannya adalah \(\color{blue} x\leq -1 \text{ atau } x \geq 1\)
(4) \(5x \:-\:16\leq -6 \text{ dan } 2x \:-\: 1\geq -5\)
\(5x \:-\:16\leq -6\)
\(5x \leq -6 + 16\)
\(5x \leq 10\)
\(x \leq \dfrac{10}{5}\)
\(x \leq 2\)
\(\text{ dan (irisan)}\)
\(2x – 1\geq -5\)
\(2x \geq -5 + 1\)
\(2x \geq -4\)
\(x \geq -\dfrac{4}{2}\)
\(x \geq -2\)
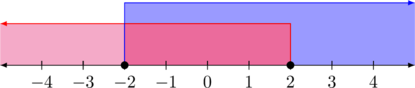
Solusi pertidaksamaannya adalah \(\color{blue} -2\leq x \leq 2\)
Pertidaksamaan Kuadrat
Berikut ini adalah contoh penyelesaian pertidaksamaan kuadrat dalam garis bilangan
(1) \(x^2 \:-\: x \:-\: 6 > 0\)
\(x^2 \:-\: x \:-\: 6 > 0\)
\(\color{blue}\text{faktorkan}\)
\((x + 2)(x \:-\:3) > 0\)
\(\text{pembuat nol:}\)
\(x + 2 = 0\rightarrow x = -2\)
\(x \:-\: 3 = 0\rightarrow x = 3\)
Gambar garis bilangan dan tandai angka \(-2\) dan \(3\) dengan lingkaran kecil putih karena \(-2\) dan \(3\) tidak ikut menjadi solusi pertidaksamaan (tanda pertidaksamaan \(>\) tidak pakai sama dengan).
Untuk tes tanda, mulailah dari daerah paling kanan
Ambil angka sebarang, misalnya angka 4, kemudian masukkan angka 4 dalam \((x + 2)(x – 3)\) dan hasilnya \((4 + 2)(4 – 3)\) positif (tidak perlu sampai hasil akhir, yang kita butuhkan hanya tanda hasilnya saja)
Untuk tanda sebelah kiri pembuat nol 3, kita lihat bahwa 3 berasal dari \((x – 3)^1\) faktor pangkat ganjil, sehingga tanda sebelah kiri angka 3 harus berubah tanda menjadi negatif
Selanjutnya, untuk tanda sebelah kiri pembuat nol −2, kita lihat bahwa −2 berasal dari \((x + 2)^1\) faktor pangkat ganjil, sehingga tanda sebelah kiri angka −2 harus berubah tanda menjadi positif
Setelah semua daerah kita tandai, solusi pertidaksamaan \((x + 2)(x – 3) > 0\) adalah daerah yang bertanda positif

Solusi pertidaksamaannya adalah \(x < -2 \text{ atau } x > 3\)
(2) \(x^2 \:-\:2x +1 \geq 0\)
\(x^2\:-\:2x +1 \geq 0\:\:\:\:\:\color{blue}\text{faktorkan}\)
\((x \:-\: 1)(x\:-\: 1) \geq 0\)
\((x \:-\: 1)^2 \geq 0\)
\(\text{pembuat nol:}\)
\(x\:-\:1 = 0\rightarrow x = 1\)
Gambar garis bilangan dan tandai angka \(1\) dengan lingkaran kecil hitam karena \(1\) ikut menjadi solusi pertidaksamaan (tanda pertidaksamaan \(\geq\) memuat tanda sama dengan).
Untuk tes tanda, mulailah dari daerah paling kanan
Ambil angka sebarang, misalnya angka 2, kemudian masukkan angka 2 dalam \((x\:-\: 1)^2\) dan hasilnya \((2\:-\:1)^2\) positif
Untuk tanda sebelah kiri pembuat nol 1, kita lihat bahwa 1 berasal dari \((x \:-\: 1)^2\) faktor pangkat genap, sehingga tanda sebelah kiri angka 1 tidak berubah, tetap positif

Solusi pertidaksamaannya adalah \(x \in \Re\) (semua x anggota bilangan real memenuhi)
Pertidaksamaan Rasional
(1) \(\dfrac{x + 2}{x \:-\: 3} \leq 0\)
\(\text{pembuat nol:}\)
\(x + 2 = 0\rightarrow x = -2\)
\(x \:-\: 3 \neq 0\rightarrow x \neq 3\)
Gambar garis bilangan dan tandai angka \(-2\) dengan lingkaran kecil hitam dan \(3\) dengan lingkaran kecil putih (karena \(x \neq 3\))
Untuk tes tanda, mulailah dari daerah paling kanan
Ambil angka sebarang, misalnya angka 4, kemudian masukkan angka 4 dalam \(\dfrac{x + 2}{x \:-\: 3}\) dan hasilnya \(\dfrac{4 + 2}{4\:-\: 3}\) positif
Untuk tanda sebelah kiri pembuat nol 3, kita lihat bahwa 3 berasal dari \((x\:-\: 3)^1\) faktor pangkat ganjil, sehingga tanda sebelah kiri angka 3 harus berubah tanda menjadi negatif
Selanjutnya, untuk tanda sebelah kiri pembuat nol −2, kita lihat bahwa −2 berasal dari \((x + 2)^1\) faktor pangkat ganjil, sehingga tanda sebelah kiri angka −2 harus berubah tanda menjadi positif
Setelah semua daerah kita tandai, solusi pertidaksamaan \(\dfrac{x + 2}{x \:-\:3} \leq 0\) adalah daerah yang bertanda negatif

Solusi pertidaksamaannya adalah \(\color{blue} -2\leq x < 3\)
(2) \(\dfrac{x + 2}{x \:-\:2} \geq 3\)
\(\dfrac{x + 2}{x \:-\: 2} \geq 3\)
\(\dfrac{x + 2}{x \:-\: 2} – 3 \geq 0\)
\(\color{blue}\text{samakan penyebut}\)
\(\dfrac{x + 2}{x \:-\: 2} – \dfrac{3(x\:-\:2)}{x\:-\:2} \geq 0\)
\(\dfrac{x + 2\:-\:3(x\:-\:2)}{x\:-\: 2} \geq 0\)
\(\dfrac{x + 2 \:-\:3x + 6}{x \:-\: 2} \geq 0\)
\(\dfrac{-2x + 8}{x \:-\:2} \geq 0\)
\(\text{pembuat nol:}\)
\(-2x + 8 = 0\rightarrow x = 4\)
\(x \:-\: 2 \neq 0\rightarrow x \neq 2\)
Gambar garis bilangan dan tandai angka \(4\) dengan lingkaran kecil hitam dan \(2\) dengan lingkaran kecil putih (karena \(x \neq 2\))
Untuk tes tanda, mulailah dari daerah paling kanan
Ambil angka sebarang, misalnya angka 5, kemudian masukkan angka 5 dalam \(\dfrac{-2x + 8}{x\:-\: 2}\) dan hasilnya \(\dfrac{-2(5) + 8}{5 \:-\:2}\) negatif
Untuk tanda sebelah kiri pembuat nol 4, kita lihat bahwa 4 berasal dari \((-2x + 8)^1\) faktor pangkat ganjil, sehingga tanda sebelah kiri angka 4 harus berubah tanda menjadi positif
Selanjutnya, untuk tanda sebelah kiri pembuat nol 2, kita lihat bahwa 2 berasal dari \((x \:-\: 2)^1\) faktor pangkat ganjil, sehingga tanda sebelah kiri angka 2 harus berubah tanda menjadi negatif
Setelah semua daerah kita tandai, solusi pertidaksamaan \(\dfrac{-2x + 8}{x \:-\:2} \geq 0\) adalah daerah yang bertanda positif

Solusi pertidaksamaannya adalah \(\color{blue} 2 < x \leq 4\)
(3) \(\dfrac{(x+1)^2}{x \:-\: 5} < 0\)
\(\dfrac{(x+1)^2}{x \:-\: 5} < 0\)
\(\text{pembuat nol:}\)
\(x + 1 = 0\rightarrow x = -1\)
\(x\:-\: 5 \neq 0\rightarrow x \neq 5\)
Gambar garis bilangan dan tandai angka \(-1\) dengan lingkaran kecil putih (tanda pertidaksamaan \(<\) tidak pakai sama dengan) dan \(5\) dengan lingkaran kecil putih (karena \(x \neq 5\))
Untuk tes tanda, mulailah dari daerah paling kanan
Ambil angka sebarang, misalnya angka 6, kemudian masukkan angka 6 dalam \(\dfrac{(x+1)^2}{x \:-\: 5}\) dan hasilnya \(\dfrac{(6+1)^2}{6 \:-\: 5}\) positif
Untuk tanda sebelah kiri pembuat nol 5, kita lihat bahwa 5 berasal dari \((x\:-\:5)^1\) faktor pangkat ganjil, sehingga tanda sebelah kiri angka 5 harus berubah tanda menjadi negatif
Selanjutnya, untuk tanda sebelah kiri pembuat nol \(-1\), kita lihat bahwa \(-1\) berasal dari \((x + 1)^2\) faktor pangkat genap, sehingga tanda sebelah kiri angka \(-1\) tanda tetap sama yaitu negatif
Setelah semua daerah kita tandai, solusi pertidaksamaan \(\dfrac{(x+1)^2}{x \:-\: 5} < 0\) adalah daerah yang bertanda negatif

Solusi pertidaksamaannya adalah \(\color{blue} x < 5, x \neq -1\)
(4) \(\dfrac{(x\:-\:1)^4\:(x\:-\:3)}{x^2 + 6x + 8} \geq 0\)
\(\dfrac{(x\:-\:1)^4\:(x\:-\:3)}{x^2 + 6x + 8} \geq 0\)
\(\dfrac{(x\:-\:1)^4\:(x\:-\:3)}{(x + 2)(x + 4)} \geq 0\)
\(\text{pembuat nol:}\)
\(x\:-\:1 = 0\rightarrow x = 1\)
\(x\:-\:3= 0\rightarrow x = 3\)
\(x + 2 \neq 0\rightarrow x \neq -2\)
\(x + 4 \neq 0\rightarrow x \neq -4\)
Gambar garis bilangan dan tandai angka \(1\) dan \(3\) dengan lingkaran kecil hitam, dan \(-2\) dan \(-4\) dengan lingkaran kecil putih
Untuk tes tanda, mulailah dari daerah paling kanan
Ambil angka sebarang, misalnya angka 4, kemudian masukkan angka 4 dalam \(\dfrac{(x\:-\:1)^4\:(x\:-\:3)}{(x + 2)(x + 4)}\) dan hasilnya \(\dfrac{(4\:-\:1)^4\:(4\:-\:3)}{(4 + 2)(4 + 4)}\) positif
Untuk tanda sebelah kiri pembuat nol 3, kita lihat bahwa 3 berasal dari \((x\:-\:3)^1\) faktor pangkat ganjil, sehingga tanda sebelah kiri angka 3 harus berubah tanda menjadi negatif
Untuk tanda sebelah kiri pembuat nol 1, kita lihat bahwa 1 berasal dari \((x \:-\:1)^4\) faktor pangkat genap, sehingga tanda sebelah kiri angka 1 tanda tetap sama yaitu negatif
Untuk tanda sebelah kiri pembuat nol \(-2\), kita lihat bahwa \(-2\) berasal dari \((x+2)^1\) faktor pangkat ganjil, sehingga tanda sebelah kiri angka \(-2\) harus berubah tanda menjadi positif
Selanjutnya, untuk tanda sebelah kiri pembuat nol \(-4\), kita lihat bahwa \(-4\) berasal dari \((x+4)^1\) faktor pangkat ganjil, sehingga tanda sebelah kiri angka \(-4\) harus berubah tanda menjadi negatif
Setelah semua daerah kita tandai, solusi pertidaksamaan \(\dfrac{(x\:-\:1)^4\:(x\:-\:3)}{(x + 2)(x + 4)} \geq 0\) adalah daerah yang bertanda positif
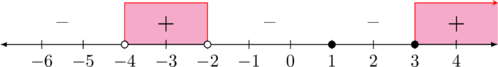
Solusi pertidaksamaannya adalah \(\color{blue} -4 < x < -2, x = 1, \text{ atau } x \geq 3\)
(5) \(\dfrac{(x^2 \:-\: 4)(x^2\:-\: x + 30)}{x^3 \:-\: x^2} \geq 0\)
\(\dfrac{(x^2 \:-\: 4)(x^2\:-\: x + 30)}{x^3 \:-\: x^2} \geq 0\:\:\:\:\:\color{blue}\text{faktorkan}\)
\(\dfrac{(x + 2)(x\:-\: 2)(x^2 \:-\: x + 30)}{x^2(x \:-\: 1)} \geq 0\)
Note:
Untuk \(x^2 \:-\: x + 30\) tidak difaktorkan, karena definit positif
Syarat definit positif :
- \(a > 0\)
- \(b^2\:-\: 4ac < 0\)
Sehingga \(x^2 \:-\: x + 30\) nilainya selalu positif untuk setiap \(x \in \Re\)
\(\text{pembuat nol:}\)
\(x + 2= 0\rightarrow x = -2\)
\(x \:-\: 2= 0\rightarrow x = 2\)
\(x^2 \neq 0\rightarrow x \neq 0\)
\(x \:-\: 1 \neq 0\rightarrow x \neq 1\)
Gambar garis bilangan dan tandai angka \(2\) dan \(-2\) dengan lingkaran kecil hitam, dan \(0\) dan \(1\) dengan lingkaran kecil putih
Untuk tes tanda, mulailah dari daerah paling kanan
Ambil angka sebarang, misalnya angka 3, kemudian masukkan angka 3 dalam \(\dfrac{(x + 2)(x\:-\: 2)(x^2 \:-\:x + 30)}{x^2(x \:-\: 1)} \) dan hasilnya \(\dfrac{(3 + 2)(3 \:-\: 2)(+++)}{3^2(3 \:-\:1)} \) positif
Untuk tanda sebelah kiri pembuat nol 2, kita lihat bahwa 2 berasal dari \((x \:-\:2)^1\) faktor pangkat ganjil, sehingga tanda sebelah kiri angka 2 harus berubah tanda menjadi negatif
Untuk tanda sebelah kiri pembuat nol 1, kita lihat bahwa 1 berasal dari \((x\:-\:1)^1\) faktor pangkat ganjil, sehingga tanda sebelah kiri angka 1 harus berubah tanda menjadi positif
Untuk tanda sebelah kiri pembuat nol 0, kita lihat bahwa 0 berasal dari \(x^2\) faktor pangkat genap, sehingga tanda sebelah kiri angka 0 tidak berubah (tetap sama) yaitu positif
Selanjutnya, untuk tanda sebelah kiri pembuat nol \(-2\), kita lihat bahwa \(-2\) berasal dari \((x + 2)^1\) faktor pangkat ganjil, sehingga tanda sebelah kiri angka \(-2\) harus berubah tanda menjadi negatif
Setelah semua daerah kita tandai, solusi pertidaksamaan \(\dfrac{(x + 2)(x \:-\:2)(x^2 \:-\:x + 30)}{x^2(x \:-\:1)} \geq 0\) adalah daerah yang bertanda positif

Solusi pertidaksamaannya adalah \(\color{blue} -2 \leq x < 1, x \neq 0, \text{ atau } x \geq 2\)
