A. Pola Bilangan Persegi
Berikut ini adalah gambar persegi identik yang disusun menjadi suatu pola persegi.
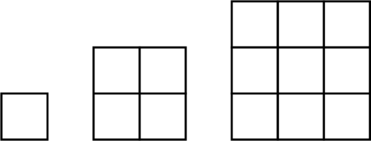
Pola ke-1: \(1^2 = 1 \text{ kotak}\)
Pola ke-2: \(2^2 = 4 \text{ kotak}\)
Pola ke-3: \(3^2 = 9 \text{ kotak}\)
…
Pola ke-\(n\): \(n^2\)
Jadi, rumus untuk suku ke-\(n\) pada pola bilangan persegi adalah \(n^2\)
B. Pola Bilangan Persegi Panjang
Berikut ini adalah gambar persegi identik yang disusun menjadi suatu pola persegi panjang.
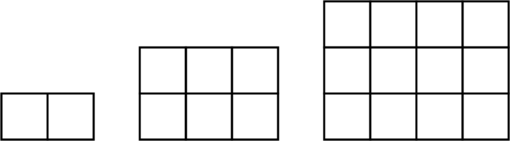
Pola ke-1: \((1 + 1)1 = 2 \text{ kotak}\)
Pola ke-2: \((2 + 1) 2= 6 \text{ kotak}\)
Pola ke-3: \((3 + 1)3 = 12 \text{ kotak}\)
…
Pola ke-\(n\): \((n + 1)n\) atau bisa ditulis \(n^2 + n\)
Jadi, rumus untuk untuk suku ke-\(n\) pada pola bilangan persegi panjang adalah \(n^2 + n\)
C. Pola Bilangan Segitiga
Pola Segitiga Sama Sisi
Berikut ini adalah gambar segitiga sama sisi identik yang disusun menjadi suatu pola segitiga sama sisi.
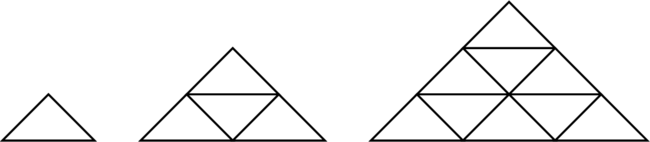
Pola ke-1: \(1^2 = 1 \text{ segitiga sama sisi}\)
Pola ke-2: \(2^2 = 4\text{ segitiga sama sisi}\)
Pola ke-3: \(3^2 = 9 \text{ segitiga sama sisi}\)
…
Pola ke-\(n\): \(n^2\)
Jadi, banyaknya segitiga sama sisi identik pada pola ke-\(n\) adalah \(n^2\)
Berikut ini adalah gambar lingkaran identik yang disusun menjadi suatu pola segitiga sama sisi.

Pola ke-1: \(\dfrac{(1 + 1)1}{2} = 1 \text{ lingkaran}\)
Pola ke-2: \(\dfrac{(2 + 1)2}{2} = 3 \text{ lingkaran}\)
Pola ke-3: \(\dfrac{(3 + 1)3}{2} = 6\text{ lingkaran}\)
…
Pola ke-\(n\): \(\dfrac{(n + 1)n}{2}\) atau dapat ditulis \(\dfrac{n^2 + n}{2}\)
Jadi, banyaknya lingkaran pada pola ke-\(n\) adalah \(\dfrac{n^2 + n}{2}\)
D. Pola Bilangan Fibonacci
Contoh 1:
\(0, 1, 1, 2, 3, 5, 8, 13, 21, 34, \dotso\)
Barisan ini dimulai dengan angka 0 dan 1, dan suku-suku berikutnya dihasilkan dari penjumlahan dua suku sebelumnya.
1 berasal dari 0 + 1
2 berasal dari 1 + 1
3 berasal dari 1 + 2
5 berasal dari 2 + 3
8 berasal dari 3 + 5 dan seterusnya
Contoh 2:
\(1, 1, 2, 3, 5, 8, 13, 21, 34, \dotso\)
Barisan ini dimulai dengan angka 1 dan 1, dan suku-suku berikutnya dihasilkan dari penjumlahan dua suku sebelumnya.
2 berasal dari 1 + 1
3 berasal dari 1 + 2
5 berasal dari 2 + 3
8 berasal dari 3 + 5 dan seterusnya
E. Pola Barisan Aritmetika
Suatu barisan bilangan disebut barisan aritmetika jika selisih (beda) antara dua suku yang berurutan selalu sama.
Contoh barisan aritmetika naik.
\(3, 6, 9, 12, 15, 18, 21, 24, 27, 30, \dotso\)
Suku pertama = 3
Beda = 3
Contoh barisan aritmetika turun.
\(5, 3, 1, -1, -3, -5, -7, -9, \dotso\)
Suku pertama = 5
Beda = \(-2\)
Rumus suku ke-\(n\)
\(\text{U}_n = a + (n \:-\:1)b\)
Dengan \(a\) adalah suku pertama dan \(b\) adalah beda
\(\text{Beda} = \text{U}_n \:-\:\text{U}_{(n-1)}\)
Rumus jumlah \(n\) suku pertama
\(\text{U}_1 + \text{U}_2 + \text{U}_3 + \dotso + \text{U}_n\)
\(\text{S}_n = \dfrac{n}{2}(a + \text{U}_n)\)
atau dapat ditulis
\(\text{S}_n = \dfrac{n}{2}(2a + (n \:-\:1)b)\)
Contoh soal:
Terdapat barisan aritmetika \(5, 10, 15, 20, 25, \dotso\)
Tentukan:
(a) Rumus umum suku ke-\(n\)
(b) Suku ke-20
(c) Jumlah 20 suku pertama
Penyelesaian:
Pada barisan \(5, 10, 15, 20, 25, \dotso\) yang menjadi suku pertama (\(a\)) adalah 5.
Beda = 10 – 5 = 5
(a) Rumus umum suku ke-\(n\)
\(\text{U}_n = a + (n \:-\:1)b\)
\(\text{U}_n = 5 + (n \:-\:1)5\)
\(\text{U}_n = 5 + 5n \:-\:5\)
\(\text{U}_n = 5n\)
(b) Suku ke-20
\(\text{U}_{20}= 5(20) = 100\)
(c) Jumlah 20 suku pertama
\(\text{S}_{n} = \dfrac{n}{2}(a + \text{U}_{n})\)
\(\text{S}_{20} = \dfrac{20}{2}(5 + \text{U}_{20})\)
\(\text{S}_{20} = \dfrac{20}{2}(5 + 100)\)
\(\text{S}_{20} = 10(105)\)
\(\text{S}_{20} = 1.050\)
F. Pola Barisan Geometri
Suatu barisan bilangan disebut barisan geometri jika rasio antara dua suku yang berurutan selalu sama.
\(\text{Rasio} = \dfrac{\text{U}_{(n + 1)}}{\text{U}_n}\)
Contoh:
\(2, 8, 32, 128, 512, 2048, \dotso\)
Suku pertama = 2
Rasio = \(\dfrac{\text{U}_2}{\text{U}_1} = \dfrac{8}{2} = 4\)
Rumus suku ke-\(n\)
\(\text{U}_n = a\cdot r^{n\:-\:1}\)
Rumus jumlah \(n\) suku pertama
\(\text{S}_n = \dfrac{a(r^n \:-\:1)}{r \:-\:1}\)
Contoh soal:
Terdapat barisan geometri \(3, 15, 75, 375, 1875\dotso\)
Tentukan:
(a) Rumus umum suku ke-\(n\)
(b) Suku ke-8
(c) Jumlah 8 suku pertama
Penyelesaian:
Pada barisan \(3, 15, 75, 375, 1875\dotso\) yang menjadi suku pertama (\(a\)) adalah 3.
rasio = \(\dfrac{15}{3} = 5\)
(a) Rumus umum suku ke-\(n\)
\(\text{U}_n = a\cdot r^{n\:-\:1}\)
\(\text{U}_n = 3\cdot 5^{n\:-\:1}\)
(b) Suku ke-8
\(\text{U}_8 = 3\cdot 5^{8\:-\:1}\)
\(\text{U}_8 = 3\cdot 5^{7}\)
\(\text{U}_8 = 3(78.125)\)
\(\text{U}_8 = 234.375\)
(c) Jumlah 8 suku pertama
\(\text{S}_{n} =\dfrac{a(r^n \:-\:1)}{r \:-\:1}\)
\(\text{S}_{8} =\dfrac{3(5^8 \:-\:1)}{5 \:-\:1}\)
\(\text{S}_{8} =\dfrac{3(390.625 \:-\:1)}{4}\)
\(\text{S}_{8} =\dfrac{3(390.624)}{4}\)
\(\text{S}_{8} =3(97.656)\)
\(\text{S}_{8} =292.968\)
