Bentuk umum polinomial:
\(\color{blue} \text{f}(x) = a_n x^n + a_{n\:-\:1}x^{n\:-\:1} + a_{n\:-\:2}x^{n\:-\:2} + \dotso + a_2x^2 + a_1x + a_0\)
Contoh:
\(\text{f}(x) = 5x^3 \:-\:2x^2 + x + 12\)
\(\text{g}(x) = 2x^5 + x^4 \:-\: 15x^3\:-\:1\)
Suatu polinomial selalu dapat dinyatakan sebagai pembagi dikali hasil bagi ditambah sisa.
\(\color{blue} \text{f}(x) = \text{pembagi}\times \text{ hasil bagi} + \text{ sisa}\)
\(\color{blue} \text{f}(x) = \text{p}(x)\times \text{h}(x) + \text{s}(x)\)
Contoh:
Polinomial \(\text{f}(x) = 2x^3 + 5x^2 \:-\:x + 10\) jika dibagi oleh \(x\:-\:2\) menghasilkan hasil bagi \(2x^2 + 9x + 17\) dan sisa 44.
Polinomial \(\text{f}(x)\) dapat dinyatakan sebagai berikut:
\(\text{f}(x)= (x\:-\:2)\cdot (2x^2 + 9x + 17) + 44\)
Bukti:
\(\text{f}(x)= 2x^3 + 9x^2 + 17x\:-\:4x^2\:-\:18x \:-\:34 + 44\)
\(\text{f}(x)= 2x^3 + 5x^2 \:-\:x + 10\)
Cara menentukan nilai polinomial
Untuk menentukan nilai dari suatu polinomial dapat digunakan cara langsung atau dengan metode Horner.
1. Cara Langsung
Contoh 1:
Tentukan nilai \(\text{f}(x) = 5x^3 \:-\:x^2 \:-\:2x + 4\) untuk\(x = 1\).
\(\text{f}(1) = 5(1)^3 \:-\:(1)^2 \:-\:2(1)+ 4\)
\(\text{f}(1) = 5 \:-\:1 \:-\:2+ 4\)
\(\text{f}(1) = 6\)
Contoh 2:
Tentukan nilai \(\text{g}(x) = 2x^5 + x^3 \:-\:13x^2 \:-\:x + 1\) untuk\(x = -2\).
\(\text{g}(-2) = 2(-2)^5 + (-2)^3 \:-\:13(-2)^2 \:-\:(-2) + 1\)
\(\text{g}(-2) = 2(-32) \:-\:8 \:-\:13(4) + 2 + 1\)
\(\text{g}(-2) = -64 \:-\:8 \:-\:52 + 2 + 1\)
\(\text{g}(-2) = -121\)
2. Metode Horner
Contoh 1:
Tentukan nilai \(\text{f}(x) = 5x^3 \:-\:x^2 \:-\:2x + 4\) untuk \(x = 1\).
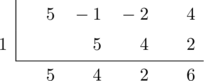
Nilai \(\text{f}(x) = 5x^3 \:-\:x^2 \:-\:2x + 4\) untuk \(x = 1\) ditunjukkan oleh angka pada baris terakhir paling kanan, yaitu 6.
Contoh 2:
Tentukan nilai \(\text{g}(x) = 2x^5 + x^3 \:-\:13x^2 \:-\:x + 1\) untuk \(x = -2\).
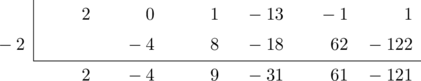
Nilai \(\text{g}(x) = 2x^5 + x^3 \:-\:13x^2 \:-\:x + 1\) untuk \(x = -2\) ditunjukkan oleh angka pada baris terakhir paling kanan, yaitu −121.
