Terdapat 2 cara untuk menentukan hasil bagi polinomial, yaitu dengan cara pembagian biasa dan dengan metode Horner.
1. Cara Pembagian Biasa
Contoh 1
Tentukan hasil bagi suku banyak \(\text{f}(x) = 2x^3\:-\:15x^2 + 28x \:-\:15\) oleh \(x\:-\:5\).
Dari bagan di atas, jika \(\text{f}(x) = 2x^3\:-\:15x^2 + 28x \:-\:15\) dibagi oleh \(x\:-\:5\) akan menghasilkan hasil bagi \(2x^2\:-\:5x + 3\).
Contoh 2
Tentukan hasil bagi suku banyak \(\text{g}(x) = x^6 + 3x^5\:-\:x\:-\:3\) oleh \(x + 3\).
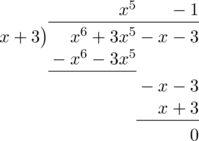
Dari bagan di atas, jika \(\text{g}(x) = x^6 + 3x^5\:-\:x\:-\:3\) dibagi oleh \(x + 3\) akan menghasilkan hasil bagi \(x^5\:-\:1\).
Contoh 3
Tentukan hasil bagi suku banyak \(\text{h}(x) = 2x^4 + 5x^3 + 4x^2 + 8x\:-\:5\) oleh \(2x + 5\).
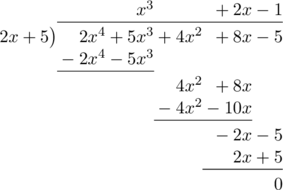
Dari bagan di atas, jika \(\text{h}(x) = 2x^4 + 5x^3 + 4x^2 + 8x\:-\:5\) dibagi oleh \(2x + 5\) akan menghasilkan hasil bagi \(x^3 + 2x\:-\;1\).
2. Metode Horner
Contoh 1
Tentukan hasil bagi suku banyak \(\text{f}(x) = 2x^3\:-\:15x^2 + 28x \:-\:15\) oleh \(x\:-\:5\).
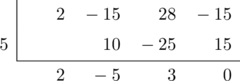
Hasil pembagian polinomial pangkat tiga oleh \(x\:-\:5\) akan menghasilkan persamaan pangkat dua.
Koefisien persamaan pangkat dua ditunjukkan oleh deretan angka pada baris terakhir yaitu 2, −5, 3.
Jadi, hasil baginya adalah \(2x^2\:-\:5x + 3\)
Catatan: angka 0 adalah sisa pembagian
Contoh 2
Tentukan hasil bagi suku banyak \(\text{g}(x) = x^6 + 3x^5\:-\:x\:-\:3\) oleh \(x + 3\).
Hasil pembagian polinomial pangkat enam oleh \(x + 3\) akan menghasilkan polinomial pangkat lima.
Koefisien polinom pangkat lima ditunjukkan oleh deretan angka pada baris terakhir yaitu 1, 0, 0, 0, 0, −1.
Jadi, hasil baginya adalah \(x^5\:-\:1\)
Contoh 3
Tentukan hasil bagi suku banyak \(\text{h}(x) = 2x^4 + 5x^3 + 4x^2 + 8x\:-\:5\) oleh \(2x + 5\).
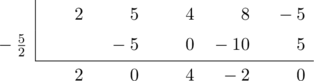
Hasil pembagian polinomial pangkat empat oleh \(2x + 5\) akan menghasilkan polinomial pangkat tiga.
Koefisien pangkat tiga awal: 2, 0, 4, −2
Karena pembaginya adalah \(\color{red}2\color{black}x + 5\) (koefisien x adalah 2), maka hasil baginya harus dibagi 2.
Koefisien pangkat tiga hasil: 1, 0, 2, −1
Jadi, hasil baginya adalah \(x^3 + 2x \:-\:1\)
LATIHAN SOAL
Soal 01
Diketahui \(\dfrac{4x^6\:-\:6x^5 \:-\:7x^3 + 10x^2 \:-\:9x + 2}{2x\:-\:1} = h(x) + \dfrac{r}{2x\:-\:1}\), nilai \(h(r) = \dotso\)
(A) \(-12\)
(B) \(-13\)
(C) \(1\)
(D) \(12\)
(E) \(13\)
Soal 02
Diketahui \(\dfrac{x^{150} \:-\:y^{150}}{x^5 + y^5}\), suku ke-10 adalah…
(A) \(-x^{100}y^{45}\)
(B) \(x^{100}y^{45}\)
(C) \(-x^{105}y^{50}\)
(D) \(x^{105}y^{50}\)
(E) \(-x^{125}y^{60}\)