Quiz-summary
0 of 11 questions completed
Pertanyaan:
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
Information
Dear Students,
Welcome to today’s quiz! This is your opportunity to demonstrate what you’ve learned so far, so do your best. Please keep in mind that you have a maximum of 60 minutes to complete all the questions. Make sure to manage your time wisely and answer each question thoughtfully.
Good luck!
Anda telah menyelesaikan kuis sebelumnya. Oleh karena itu, Anda tidak dapat memulainya lagi.
Quiz is loading...
You must sign in or sign up to start the quiz.
You have to finish following quiz, to start this quiz:
Hasil
0 dari 11 pertanyaan terjawab dengan benar
Waktu Anda:
Time has elapsed
Anda telah meraih 0 dari 0 poin, (0)
Categories
- Not categorized 0%
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- Dijawab
- Ragu-Ragu
-
Pertanyaan 1 dari 11
1. Pertanyaan
1 pointsSisa pembagian \(x^{17}\:-\:2x^{11} + 3x^4 \:-\:x^2 + 4\) oleh \(x \:-\:x^3\) adalah…
Benar
Misal \(f(x) = x^{17}\:-\:2x^{11} + 3x^4 \:-\:x^2 + 4\)
\(f(x) = (x\:-\:x^3)H(x) + (ax^2 + bx + c)\)
dengan \(H(x)\) = hasil bagi dan \(ax^2 + bx+ c\) = sisa pembagian
\(f(x) = x(1 + x)(1\:-\:x)H(x) + (ax^2 + bx + c)\)
pilih x = 0
\(f(0) = 0(1 + 0)(1\:-\:0)H(0) + (a\cdot 0^2 + b \cdot 0 + c)\)
\(4 = c\)
Pilih x = −1
\(f(-1) = a\:-\:b + c\)
\(7 = a\:-\:b + 4\)
\(3 = a\:-\:b\dotso \color{red} (1)\)
Pilih x = 1
\(f(1) = a + b + c\)
\(5 = a + b + 4\)
\(1 = a + b \dotso \color{red} (2)\)
Elimininasi persamaan (1) dan (2) sehingga didapatkan \(a = 2 \text{ dan } b = -1\)
Jadi, sisa pembagiannya adalah \(2x^2 \:-\:x + 4\)
Salah
Misal \(f(x) = x^{17}\:-\:2x^{11} + 3x^4 \:-\:x^2 + 4\)
\(f(x) = (x\:-\:x^3)H(x) + (ax^2 + bx + c)\)
dengan \(H(x)\) = hasil bagi dan \(ax^2 + bx+ c\) = sisa pembagian
\(f(x) = x(1 + x)(1\:-\:x)H(x) + (ax^2 + bx + c)\)
pilih x = 0
\(f(0) = 0(1 + 0)(1\:-\:0)H(0) + (a\cdot 0^2 + b \cdot 0 + c)\)
\(4 = c\)
Pilih x = −1
\(f(-1) = a\:-\:b + c\)
\(7 = a\:-\:b + 4\)
\(3 = a\:-\:b\dotso \color{red} (1)\)
Pilih x = 1
\(f(1) = a + b + c\)
\(5 = a + b + 4\)
\(1 = a + b \dotso \color{red} (2)\)
Elimininasi persamaan (1) dan (2) sehingga didapatkan \(a = 2 \text{ dan } b = -1\)
Jadi, sisa pembagiannya adalah \(2x^2 \:-\:x + 4\)
-
Pertanyaan 2 dari 11
2. Pertanyaan
1 pointsHasil bagi \(4x^4 \:-\:2x^3 + 5x + 6\) oleh \(2x^2 + 9x + 2\) adalah…
Benar
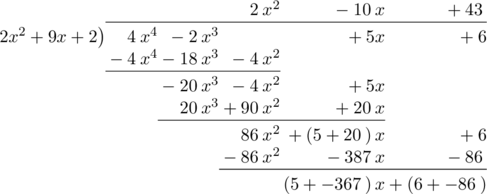
Jadi, hasil baginya adalah \(2x^2 \:-\:10x +43\)
Salah
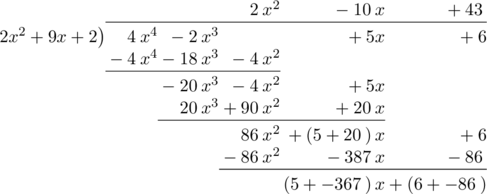
Jadi, hasil baginya adalah \(2x^2 \:-\:10x +43\)
-
Pertanyaan 3 dari 11
3. Pertanyaan
1 pointsSalah satu faktor polinomial \(f(x) = x^4 \:-\:15x^2 \:-\:10x + n\) adalah \(x + 2\). Faktor yang lainnya adalah…
Benar
Karena x + 2 adalah faktor dari polinomial f(x), maka berlaku f(−2) = 0
\((-2)^4 \:-\:15(-2)^2 \:-\:10(-2) + n = 0\)
\(16 \:-\:60 + 20 + n = 0\)
\(n = 24\)
Polinomial tersebut adalah \(f(x) = x^4\:-\:15x^2 \:-\:10x + 24\)
Selanjutnya bagi polinomial f(x) dengan x + 2 untuk mendapatkan faktor-faktor yang lain
Faktor-faktor yang lain diperoleh dari hasil baginya, yaitu (x − 1)(x − 4)(x + 3)
Salah
Karena x + 2 adalah faktor dari polinomial f(x), maka berlaku f(−2) = 0
\((-2)^4 \:-\:15(-2)^2 \:-\:10(-2) + n = 0\)
\(16 \:-\:60 + 20 + n = 0\)
\(n = 24\)
Polinomial tersebut adalah \(f(x) = x^4\:-\:15x^2 \:-\:10x + 24\)
Selanjutnya bagi polinomial f(x) dengan x + 2 untuk mendapatkan faktor-faktor yang lain
Faktor-faktor yang lain diperoleh dari hasil baginya, yaitu (x − 1)(x − 4)(x + 3)
-
Pertanyaan 4 dari 11
4. Pertanyaan
1 pointsJika α, β, γ merupakan akar-akar persamaan \(x^3 \:-\:2x^2 + 3x \:-\:1 = 0\), maka persamaan baru yang akar-akarnya 1 − 2α, 1 − 2β, dan 1 − 2γ adalah…
Benar
Karena persamaan yang baru memiliki pola akar-akar yang sama, maka kita bisa menggunakan transformasi \(y = 1 \:-\: 2x\), sehingga \(x = \dfrac{1 \:-\:y}{2}\).
Substitusikan \(x = \dfrac{1 \:-\:y}{2}\) ke dalam persamaan \(x^3 \:-\:2x^2 + 3x \:-\:1 = 0\) untuk mendapatkan persamaan baru.
\(\left(\dfrac{1\:-\:y}{2} \right)^3\:-\:2\left(\dfrac{1\:-\:y}{2}\right)^2 + 3\left(\dfrac{1\:-\:y}{2}\right)\:-\:1 = 0\)
\(\dfrac{1\:-\:3y + 3y^2 \:-\:y^3}{8}\:-\:\dfrac{2(1 \:-\:2y + y^2)}{4} + \dfrac{3\:-\:3y}{2}\:-\:1=0\)
\(1\:-\:3y + 3y^2 \:-\:y^3 \:-\:4(1\:-\:2y + y^2) + 4(3\:-\:3y) \:-\:8 = 0\)
\(1\:-\:3y + 3y^2 \:-\:y^3 \:-\:4 + 8y \:-\:4y^2 + 12 \:-\:12y \:-\:8 = 0\)
\(-y^3 \:-\:y^2 \:-\:7y + 1 = 0\)
Variabel y dapat digantikan kembali menjadi variabel x
\(x^3 + x^2 + 7x \:-\:1 = 0\)
Salah
Karena persamaan yang baru memiliki pola akar-akar yang sama, maka kita bisa menggunakan transformasi \(y = 1 \:-\: 2x\), sehingga \(x = \dfrac{1 \:-\:y}{2}\).
Substitusikan \(x = \dfrac{1 \:-\:y}{2}\) ke dalam persamaan \(x^3 \:-\:2x^2 + 3x \:-\:1 = 0\) untuk mendapatkan persamaan baru.
\(\left(\dfrac{1\:-\:y}{2} \right)^3\:-\:2\left(\dfrac{1\:-\:y}{2}\right)^2 + 3\left(\dfrac{1\:-\:y}{2}\right)\:-\:1 = 0\)
\(\dfrac{1\:-\:3y + 3y^2 \:-\:y^3}{8}\:-\:\dfrac{2(1 \:-\:2y + y^2)}{4} + \dfrac{3\:-\:3y}{2}\:-\:1=0\)
\(1\:-\:3y + 3y^2 \:-\:y^3 \:-\:4(1\:-\:2y + y^2) + 4(3\:-\:3y) \:-\:8 = 0\)
\(1\:-\:3y + 3y^2 \:-\:y^3 \:-\:4 + 8y \:-\:4y^2 + 12 \:-\:12y \:-\:8 = 0\)
\(-y^3 \:-\:y^2 \:-\:7y + 1 = 0\)
Variabel y dapat digantikan kembali menjadi variabel x
\(x^3 + x^2 + 7x \:-\:1 = 0\)
-
Pertanyaan 5 dari 11
5. Pertanyaan
1 pointsSuatu suku banyak \(x^3 + ax^2 + bx + 6\), dengan \(a\) dan \(b\) konstanta, dinyatakan sebagai \(p(x)\). Jika \((x\:-\:2)\) adalah salah satu faktor dari \(p(x)\) dan saat \(p(x)\) dibagi oleh \((x\:-\:1)\) memberikan sisa 4 maka faktor-faktor linear yang lain dari \(p(x)\) adalah…
Benar
\((x\:-\:2)\) adalah salah satu faktor dari \(p(x)\), maka \(p(2) = 0\)
\(2^3 + a(2)^2 + b(2) + 6 = 0\)
\(8 + 4a + 2b + 6 = 0\)
\(4a + 2b = -14\)
\(2a + b = -7\dotso \color{red} (1)\)
\(p(x)\) dibagi oleh \((x\:-\:1)\) memberikan sisa 4, maka \(p(1) = 4\)
\(1^3 + a(1)^2 + b(1) + 6 = 4\)
\(1 + a + b + 6 = 4\)
\(a + b = -3\dotso \color{red} (2)\)
Eliminasi persamaan (1) dan (2) untuk mendapatkan \(a = -4\) dan \(b = 1\)
\(p(x) = x^3 \:-\:4x^2 + x + 6\)
Bagi \(p(x)\) dengan \(x\:-\:2\) untuk mendapatkan faktor-faktor yang lain
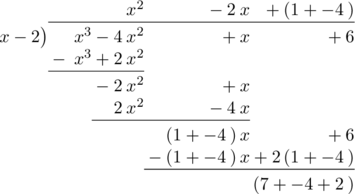
Hasil bagi = \(x^2\:-\:2x \:-\:3\)
Jadi, faktor-faktor linear yang lain = \((x \:-\:3)(x + 1)\)
Salah
\((x\:-\:2)\) adalah salah satu faktor dari \(p(x)\), maka \(p(2) = 0\)
\(2^3 + a(2)^2 + b(2) + 6 = 0\)
\(8 + 4a + 2b + 6 = 0\)
\(4a + 2b = -14\)
\(2a + b = -7\dotso \color{red} (1)\)
\(p(x)\) dibagi oleh \((x\:-\:1)\) memberikan sisa 4, maka \(p(1) = 4\)
\(1^3 + a(1)^2 + b(1) + 6 = 4\)
\(1 + a + b + 6 = 4\)
\(a + b = -3\dotso \color{red} (2)\)
Eliminasi persamaan (1) dan (2) untuk mendapatkan \(a = -4\) dan \(b = 1\)
\(p(x) = x^3 \:-\:4x^2 + x + 6\)
Bagi \(p(x)\) dengan \(x\:-\:2\) untuk mendapatkan faktor-faktor yang lain
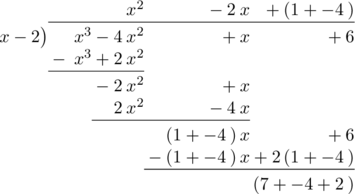
Hasil bagi = \(x^2\:-\:2x \:-\:3\)
Jadi, faktor-faktor linear yang lain = \((x \:-\:3)(x + 1)\)
-
Pertanyaan 6 dari 11
6. Pertanyaan
1 pointsJika sisa pembagian \(f(x)\) oleh \((x^2 \:-\:1)\) adalah \(-x + 3\) dan sisa pembagian \(f(x)\) oleh \((x^2 \:-\:4)\) adalah \(x + 1\), maka sisa pembagian \((x\:-\:2)f(x)\) oleh \((x^2 \:-\:x\:-\:2)\) adalah…
Benar
\(f(x)\) dibagi oleh \((x^2 \:-\:1) = (x + 1)(x\:-\:1)\) sisanya adalah \(-x + 3\)
\(f(-1) = -(-1) + 3 = 4\)
\(f(1) = -1 + 3 = 2\)
\(f(x)\) dibagi oleh \(x^2 \:-\:4) = (x + 2)(x\:-\:2)\) sisanya adalah \(x + 1\)
\(f(2) = 2 + 1 = 3\)
\(f(-2) = -2 + 1 = -1\)
\((x\:-\:2) f(x)\) dibagi oleh \(x^2 \:-\:x\:-\:2 = (x \:-\:2)(x + 1)\) sisanya \(ax + b\)
Untuk x = −1
\((-1\:-\:2)f(-1) = -a + b\)
\(-3\cdot 4 = -a + b\)
\(-a + b = -12 \dotso \color{red} (1)\)
Untuk x = 2
\((2\:-\:2)f(2) = 2a + b\)
\(0\cdot 3 = 2a + b\)
\(2a + b = 0 \dotso \color{red} (2)\)
Eliminasi persamaan (1) dan (2) untuk mendapatkan nilai \(a = 4 \) dan \(b =-8 \)
Jadi, sisa pembagiannya adalah \(4x\:-\:8\)
Salah
\(f(x)\) dibagi oleh \((x^2 \:-\:1) = (x + 1)(x\:-\:1)\) sisanya adalah \(-x + 3\)
\(f(-1) = -(-1) + 3 = 4\)
\(f(1) = -1 + 3 = 2\)
\(f(x)\) dibagi oleh \(x^2 \:-\:4) = (x + 2)(x\:-\:2)\) sisanya adalah \(x + 1\)
\(f(2) = 2 + 1 = 3\)
\(f(-2) = -2 + 1 = -1\)
\((x\:-\:2) f(x)\) dibagi oleh \(x^2 \:-\:x\:-\:2 = (x \:-\:2)(x + 1)\) sisanya \(ax + b\)
Untuk x = −1
\((-1\:-\:2)f(-1) = -a + b\)
\(-3\cdot 4 = -a + b\)
\(-a + b = -12 \dotso \color{red} (1)\)
Untuk x = 2
\((2\:-\:2)f(2) = 2a + b\)
\(0\cdot 3 = 2a + b\)
\(2a + b = 0 \dotso \color{red} (2)\)
Eliminasi persamaan (1) dan (2) untuk mendapatkan nilai \(a = 4 \) dan \(b =-8 \)
Jadi, sisa pembagiannya adalah \(4x\:-\:8\)
-
Pertanyaan 7 dari 11
7. Pertanyaan
1 pointsJika dua buah akar dari \(3x^3 + ax^2 + 6x\:-\:6 = 0\) saling berlawanan tanda, maka nilai \(a\) yang memenuhi adalah…
Benar
Misalkan \(3x^3 + ax^2 + 6x\:-\:6 = 0\) memiliki akar-akar α, β, dan γ dengan α = −β (dua akarnya saling berlawanan tanda)
α + β + γ = \(-\dfrac{b}{a}\)
−β + β + γ = \(-\dfrac{a}{3}\)
γ = \(-\dfrac{a}{3}\)
Substitusikan γ = \(-\dfrac{a}{3}\) ke \(3x^3 + ax^2 + 6x\:-\:6 = 0\)
\(3\left(-\dfrac{a}{3}\right)^3 + a\left(-\dfrac{a}{3}\right)^2 + 6\left(-\dfrac{a}{3}\right)\:-\:6 = 0\)
\(3\left(-\dfrac{a^3}{27}\right) + a\left(\dfrac{a^2}{9}\right) \:-\: \left(\dfrac{6a}{3}\right)\:-\:6 = 0\)
\(-2a\:-\:6 = 0\)
\(a = -3\)
Salah
Misalkan \(3x^3 + ax^2 + 6x\:-\:6 = 0\) memiliki akar-akar α, β, dan γ dengan α = −β (dua akarnya saling berlawanan tanda)
α + β + γ = \(-\dfrac{b}{a}\)
−β + β + γ = \(-\dfrac{a}{3}\)
γ = \(-\dfrac{a}{3}\)
Substitusikan γ = \(-\dfrac{a}{3}\) ke \(3x^3 + ax^2 + 6x\:-\:6 = 0\)
\(3\left(-\dfrac{a}{3}\right)^3 + a\left(-\dfrac{a}{3}\right)^2 + 6\left(-\dfrac{a}{3}\right)\:-\:6 = 0\)
\(3\left(-\dfrac{a^3}{27}\right) + a\left(\dfrac{a^2}{9}\right) \:-\: \left(\dfrac{6a}{3}\right)\:-\:6 = 0\)
\(-2a\:-\:6 = 0\)
\(a = -3\)
-
Pertanyaan 8 dari 11
8. Pertanyaan
1 pointsSuku banyak \(x^4 + 2x^3\:-\:5x^2 + 11x \:-\:2\) dibagi dengan \((x^2 + x\:-\:2)\) hasil baginya H(x) dan sisanya S(x), maka nilai dari H(3) − S(2) = …
Benar
\(\text{H}(x) = x^2 + x\:-\:4\)
\(\text{H}(3) = 3^2 + 3\:-\:4 = 8\)
\(\text{S}(x) = 17x\:-\:10\)
\(\text{S}(2) = 17(2) \:-\:10 = 24\)
H(3) − S(2) = −16
Salah
\(\text{H}(x) = x^2 + x\:-\:4\)
\(\text{H}(3) = 3^2 + 3\:-\:4 = 8\)
\(\text{S}(x) = 17x\:-\:10\)
\(\text{S}(2) = 17(2) \:-\:10 = 24\)
H(3) − S(2) = −16
-
Pertanyaan 9 dari 11
9. Pertanyaan
1 pointsJika \(\text{P}(x) = x^3\:-\:2x^2\:-\:4\) dan \(f(x) = 6x^4\:-\:x^2 + ax \:-\:2\). Jika kedua polinom dibagi dengan \((2x\:-\:1)\) mempunyai sisa yang sama. Nilai dari \(f(a) = \dotso\)
Benar
\(p(\frac{1}{2}) = f(\frac{1}{2})\)
\((\frac{1}{2})^3 \:-\:2(\frac{1}{2})^2\:-\:4 = 6(\frac{1}{2})^4\:-\:(\frac{1}{2})^2 + \frac{1}{2}a\:-\:2\)
\(a = -5\)
\(f(x) = 6x^4\:-\:x^2 \:-\:5x \:-\:2\)
\(f(-5) = 6(-5)^4 \:-\:(-5)^2 \:-\:5(-5)\:-\:2\)
\(f(-5) = 3748\)
Salah
\(p(\frac{1}{2}) = f(\frac{1}{2})\)
\((\frac{1}{2})^3 \:-\:2(\frac{1}{2})^2\:-\:4 = 6(\frac{1}{2})^4\:-\:(\frac{1}{2})^2 + \frac{1}{2}a\:-\:2\)
\(a = -5\)
\(f(x) = 6x^4\:-\:x^2 \:-\:5x \:-\:2\)
\(f(-5) = 6(-5)^4 \:-\:(-5)^2 \:-\:5(-5)\:-\:2\)
\(f(-5) = 3748\)
-
Pertanyaan 10 dari 11
10. Pertanyaan
1 pointsJika \(\text{P}(x) = x^4\:-\:x^3 + x^2 + 2x + b\) dibagi \((x^2 \:-\:x\:-\:2)\) bersisa \((5x + 9)\), maka sisa pembagian P(x) oleh \((2x+6)\) adalah…
Benar
Pembagi \(x^2 \:-\:x\:-\:2 = (x\:-\:2)(x + 1)\)
P(x) dibagi oleh (x − 2) bersisa P(2) = 5(2) + 9 = 19
\(2^4 \:-\:2^3 + 2^2 + 2(2) + b = 19\)
\(b = 3\)
P(x) dibagi oleh (2x + 6) bersisa P(−3)
\(\text{P}(-3) = (-3)^4\:-\:(-3)^3 + (-3)^2 + 2(-3) + 3\)
\(\text{P}(-3) = 114\)
Salah
Pembagi \(x^2 \:-\:x\:-\:2 = (x\:-\:2)(x + 1)\)
P(x) dibagi oleh (x − 2) bersisa P(2) = 5(2) + 9 = 19
\(2^4 \:-\:2^3 + 2^2 + 2(2) + b = 19\)
\(b = 3\)
P(x) dibagi oleh (2x + 6) bersisa P(−3)
\(\text{P}(-3) = (-3)^4\:-\:(-3)^3 + (-3)^2 + 2(-3) + 3\)
\(\text{P}(-3) = 114\)
-
Pertanyaan 11 dari 11
11. Pertanyaan
1 pointsP(x) adalah suku banyak berderajat 3, jika dibagi \((3x^2 + 2x + 1)\) sisanya \((6x + 7)\), dan jika dibagi \((x^2 + x\:-\:2)\) sisanya \((42x + 25)\), maka nilai dari P(2) = …
Benar
Salah
P(x) dibagi oleh \(x^2 + x \:-\:2\) sisanya \(42x + 25\)
\(\text{P}(x) = (x^2 + x\:-\:2)\cdot \text{H}(x) + (42x + 25)\)
\(\text{P}(x) = (x + 2)(x\:-\:1)\cdot \text{H}(x) + (42x + 25)\)
Ambil x = 1
\(\text{P}(1) = (1 + 2)(1\:-\:1)\cdot \text{H}(1) + (42 + 25)\)
\(\text{P}(1) = 67\)
P(x) dibagi \(3x^2 + 2x + 1\) sisanya \(6x + 7\)
\(\text{P}(x) = (3x^2 + 2x + 1)(x + a) + (6x + 7)\)
Ambil x = 1
\(\text{P}(1) = (3(1)^2 + 2(1) + 1)(1 + a) + (6(1) + 7)\)
\(67 = 6(1 + a) + 13\)
\(a = 8\)
\(\text{P}(x)= (3x^2 + 2x + 1)(x + 8) + (6x + 7)\)
\(\text{P}(2) = (3(2)^2 + 2(2) + 1)(2 + 8) + 6(2) + 7\)
\(\text{P}(2) = 189\)
