Sisa pembagian suku banyak f(x) oleh (x + a) adalah f(−a)
Contoh 1:
Tentukan sisa pembagian \(f(x) = 3x^3 \:-\:2x^2 + x\:-\:1\) oleh \(x + 2\).
Penyelesaian:
Sisa pembagian \(f(x)\) oleh \(x + 2\) adalah \(f(-2)\)
\(f(-2) = 3(-2)^3\:-\:2(-2)^2 + (-2) \:-\:1\)
\(f(-2) = 3(-8)\:-\:2(4)\:-\:2\:-\:1\)
\(f(-2) = -24\:-\:8\:-\:2\:-\:1\)
\(f(-2) = -35\)
Jadi, sisa pembagian \(f(x) = 3x^3 \:-\:2x^2 + x\:-\:1\) oleh \(x + 2\) adalah −35
Contoh 2:
Tentukan sisa pembagian \(g(x) = x^5 \:-\:4x^3\:-\:2\) oleh \(x \:-\: 1\).
Penyelesaian:
Sisa pembagian \(g(x)\) oleh \(x \:-\: 1\) adalah \(g(1)\)
\(g(1) = 1^5 \:-\:4(1)^3\:-\:2\)
\(g(1) = 1 \:-\:4\:-\:2\)
\(g(1) = -5\)
Jadi, sisa pembagian \(g(x) = x^5 \:-\:4x^3\:-\:2\) oleh \(x \:-\: 1\) adalah −5
Kita juga dapat menentukan sisa pembagian suatu polinom dengan cara pembagian biasa.
Contoh 1:
Tentukan sisa pembagian \(f(x) = 3x^3 \:-\:2x^2 + x\:-\:1\) oleh \(x + 2\).
Penyelesaian:
\(f(x) = 3x^3 \:-\:2x^2 + x\:-\:1\) dibagi oleh \(x + 2\)
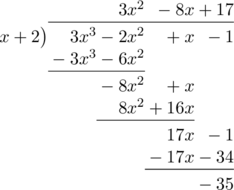
Untuk menentukan sisa pembagian \(f(x) = 3x^3 \:-\:2x^2 + x\:-\:1\) oleh \(x + 2\) lihat angka yang terdapat pada baris paling akhir, yaitu −35.
Contoh 2:
Tentukan sisa pembagian \(g(x) = x^5 \:-\:4x^3\:-\:2\) oleh \(x \:-\: 1\).
Penyelesaian:
\(g(x) = x^5 \:-\:4x^3\:-\:2\) dibagi oleh \(x \:-\: 1\).
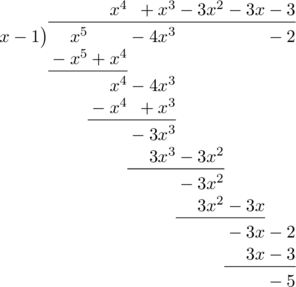
Untuk menentukan sisa pembagian \(g(x) = x^5 \:-\:4x^3\:-\:2\) oleh \(x \:-\: 1\) lihat angka yang terdapat pada baris paling akhir, yaitu −5.
Contoh 3:
Tentukan sisa pembagian \(h(x) = x^4+3x^3\:-\:2x^2 + 5\) oleh \(x^2 + 2x + 1\).
Penyelesaian:
\(h(x) = x^4+3x^3\:-\:2x^2 + 5\) dibagi oleh \(x^2 + 2x + 1\).
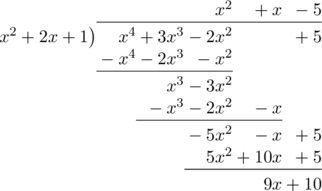
Untuk menentukan sisa pembagian \(h(x) = x^4+3x^3\:-\:2x^2 + 5\) oleh \(x^2 + 2x + 1\) lihat persamaan yang didapat pada baris paling akhir, yaitu \(9x + 10\).
Jadi, sisa pembagian \(h(x) = x^4+3x^3\:-\:2x^2 + 5\) oleh \(x^2 + 2x + 1\) adalah \(9x + 10\).
Note: derajat maksimum sisa pembagian adalah 1 lebih rendah dari derajat pembagi
Pembagi: \(x^2 + 2x + 1\) (berderajat 2)
Sisa: \(9x + 10\) (berderajat 1)
Contoh 3:
Tentukan sisa pembagian \(h(x) = 2x^4+ x^3 + 5x^2 + 10\) oleh \(x^3 + 2x^2 \:-\: x + 1\).
Penyelesaian:
\(h(x) = 2x^4+ x^3 + 5x^2 + 10\) dibagi oleh \(x^3 + 2x^2 \:-\: x + 1\)
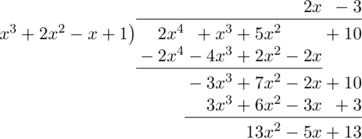
Untuk menentukan sisa pembagian \(h(x) = 2x^4+ x^3 + 5x^2 + 10\) oleh \(x^3 + 2x^2 \:-\: x + 1\) lihat persamaan yang didapat pada baris paling akhir, yaitu \(13x^2 \:-\:5x + 13\)
Jadi, sisa pembagian \(h(x) = 2x^4+ x^3 + 5x^2 + 10\) oleh \(x^3 + 2x^2 \:-\: x + 1\) adalah \(13x^2 \:-\:5x + 13\).
Note: derajat maksimum sisa pembagian adalah 1 lebih rendah dari derajat pembagi
Pembagi: \(x^3 + 2x^2 \:-\: x + 1\) (berderajat 3)
Sisa: \(13x^2 \:-\:5x + 13\) (berderajat 2)
LATIHAN SOAL
Soal 01
Jika \(f(x) = x^3\:-\:2x^2\:-\:2\) dan \(g(x) = 3x^4\:-\:2x^3\:-\:5x^2\:-\:ax\:-\:2\) bersisa sama jika dibagi \((x\:-\:2)\), maka nilai dari \(f(4) = \dotso\)
(A) \(-30\)
(B) \(-70\)
(C) 30
(D) 40
(E) 70
Jawaban: C
Dengan menggunakan teorema sisa,
\(f(2) = g(2)\)
\(2^3\:-\:2(2)^2\:-\:2 = 3(2)^4\:-\:2(2)^3 \:-\:5(2)^2\:-\:2a\:-\:2\)
\(8\:-\:8\:-\:2 = 48\:-\:16\:-\:20\:-\:2a\:-\:2\)
\(0 = 12\:-\:2a\)
\(2a = 12\)
\(a = 6\)
\(f(4) = 4^3\:-\:2(4)^2\:-\:2\)
\(f(4) = 64\:-\:32\:-\:2\)
\(f(4) = 30\)
Soal 02
Jika \(x^4 + x^3 \:-\:2x^2 + 3x + 2p = (x + 1)\cdot h(x) + 5\), dengan \(h(x)\) adalah polinom, maka nilai \(p\) adalah…
(A) \(-5\)
(B) \(-2\)
(C) \(-1\)
(D) \(4\)
(E) \(5\)
Jawaban: E
Misal \(p(x) = x^4 + x^3 \:-\:2x^2 + 3x + 2p\)
\(p(x) = (x + 1)\cdot h(x) + 5\)
\((x +1)\) disebut sebagai pembagi
\(h(x)\) disebut sebagai hasil bagi
\(5\) disebut sisa
Jadi \(p(x)\) dibagi oleh \((x + 1)\) bersisa 5
Dengan menggunakan teorema sisa dapat ditulis:
\(p(-1) = 5\)
\((-1)^4 + (-1)^3 \:-\:2(-1)^2 + 3(-1) + 2p = 5\)
\(1\:-\:1 \:-\:2\:-\:3 + 2p = 5\)
\(-5 + 2p = 5\)
\(2p = 10\)
\(p = 5\)
Soal 03
Suku banyak \(f(x)\) dibagi \((x^2 \:-\:2x)\) bersisa \((2x +1)\), dan jika dibagi \((x^2 \:-\:3x)\) bersisa \((5x + 1)\), maka sisa pembagian \(f(x)\) oleh \((x^2 \:-\:5x + 6)\) adalah…
(A) \(-22x + 49\)
(B) \(-12x + 29\)
(C) \(22x \:-\:39\)
(D) \(11x \:-\: 17\)
(E) \(12x \:-\:19\)
Jawaban: D
\(f(x)\) dibagi \((x^2 \:-\:2x)\) bersisa \((2x +1)\)
\(f(x) = (x^2 \:-\:2x)\cdot H(x) + (2x + 1)\)
\(f(x) = x(x\:-\:2)\cdot H(x) + (2x + 1)\)
Pilih \(x = 2\)
\(f(2) = 0 + 2(2) + 1\)
\(f(2) = 5\)
\(f(x) = (x^2 \:-\:3x)\cdot H(x) + (5x + 1)\)
\(f(x) = x(x\:-\:3)\cdot H(x) + (5x + 1)\)
Pilih \(x = 3\)
\(f(3) = 0 + 5(3) + 1\)
\(f(3) = 16\)
Misal \(f(x)\) dibagi oleh \((x^2 \:-\:5x + 6)\) sisanya \(\color{blue}(ax + b)\)
\(f(x) = (x^2 \:-\:5x + 6)\cdot H(x) + \color{blue} (ax + b)\)
\(f(x) = (x\:-\:3)(x\:-\:2)\cdot H(x) + \color{blue} (ax + b)\)
Pilih \(x = 2\)
\(f(2) = 0 + 2a + b\)
\(5 = 2a + b\dotso \color{red} (1)\)
Pilih \(x = 3\)
\(f(3) = 0 + 3a + b\)
\(16 = 3a + b\dotso \color{red} (2)\)
Eliminasi persamaan (1) dan (2) diperoleh \(a = 11\) dan \(b = -17\)
Jadi sisa pembagian = \(\color{blue} 11x\:-\:17\)
Soal 04
Jika \(p(x) = x^5 \:-\:x^3 + x^2 + ax + b\) dibagi \((x^2 \:-\:x\:-\:2)\) bersisa \((2x + 7)\), maka sisa pembagian \(p(x)\) oleh \((x\:-\:1)\) adalah…
(A) \(-10\)
(B) \(-9\)
(C) 9
(D) 10
(E) 11
Jawaban: B
\(p(x) = x^5 \:-\:x^3 + x^2 + ax + b\) dibagi \((x^2 \:-\:x\:-\:2)\) bersisa \((2x + 7)\)
\(p(x) = (x^2 \:-\:x\:-\:2)\cdot H(x) + (2x + 7)\)
\(p(x) = (x\:-\:2)(x + 1)\cdot H(x) + (2x + 7)\)
Pilih \(\color{blue} x = 2\)
\(p(2) = 0 + 2(2) + 7\)
\(p(2) = 11\)
\(2^5 \:-\:2^3 + 2^2 + 2a + b = 11\)
\(32\:-\:8 + 4 + 2a + b = 11\)
\(2a + b = -17 \dotso \color{red} (1)\)
Pilih \(\color{blue} x = -1\)
\(p(-1) = 0 + 2(-1) + 7\)
\(p(-1) = 5\)
\((-1)^5 \:-\:(-1)^3 + (-1)^2 \:-\:a + b = 5\)
\(-1+ 1 + 1 \:-\:a + b = 5\)
\(-a + b = 4 \dotso \color{red} (2)\)
Eliminasi persamaan (1) dan (2), diperoleh \(a = -7\) dan \(b = -3\)
Sehingga \(p(x) = x^5 \:-\:x^3 + x^2 \:-\:7x \:-\:3\)
Sisa pembagian \(p(x)\) oleh \((x\:-\:1)\) adalah \(p(1)\)
\(p(1) = 1^5 \:-\:1^3 + 1^2 \:-\:7(1)\:-\:3\)
\(p(1) = 1 \:-\:1 + 1 \:-\:7\:-\:3\)
\(p(1) = -9\)
Soal 05
\(p(x)\) adalah suku banyak berderajat 3, jika dibagi \(x^2 + 2x + 3\) bersisa \((x + 2)\) dan jika dibagi \((x^2\:-\:1)\) bersisa \((18x + 6)\), maka nilai dari \(p(3) = \dotso\)
(A) 33
(B) 104
(C) 185
(D) 199
(E) 248
Jawaban: E
\(p(x)\) dibagi \((x^2\:-\:1)\) bersisa \((18x + 6)\)
\(p(x) = (x^2\:-\:1)\cdot H(x) + (18x + 6)\)
\(p(x) = (x+1)(x\:-\:1)\cdot H(x) + (18x + 6)\)
Pilih \(\color{red} x = 1\)
\(p(1) = 0 + 18(1) + 6 \)
\(\color{blue} p(1) = 24\)
Pilih \(\color{red} x = -1\)
\(p(-1) = 0 + 18(-1) + 6 \)
\(\color{blue} p(-1) = -12\)
\(p(x)\) dibagi \(x^2 + 2x + 3\) bersisa \((x + 2)\)
\(p(x) = (x^2 + 2x + 3)\cdot H(x) + (x + 2)\)
Polinomial pangkat 3 jika dibagi \((x^2 + 2x + 3)\) menghasilkan hasil bagi dengan derajat tertingginya adalah 1, yaitu \(H(x) =ax + b\)
\(p(x) = (x^2 + 2x + 3)\cdot (ax + b) + (x + 2)\)
Pilih \(\color{red} x = 1\)
\(p(1) = (1^2 + 2(1) + 3)\cdot (a(1) + b) + (1+ 2)\)
\(24 = 6(a + b) + 3\)
\(24\:-\:3 = 6a + 6b\)
\(21 = 6a + 6b\)
Bagi kedua ruas dengan 3,
\(7= 2a + 2b \dotso \color{red} (1)\)
Pilih \(\color{red} x = -1\)
\(p(-1) = ((-1)^2 + 2(-1) + 3)\cdot (a(-1) + b) + (-1+ 2)\)
\(-12 = 2(-a + b) + 1\)
\(-13 = -2a + 2b \dotso \color{red} (2)\)
Eliminasi persamaan (1) dan (2) untuk mendapatkan nilai \(a = 5\) dan \(b = -\dfrac{3}{2}\)
Jadi polinomial \(p(x)\) dapat ditulis:
\(\color{blue} p(x) = (x^2 + 2x + 3)\cdot \left(5x \:-\: \dfrac{3}{2}\right) + (x + 2)\)
\(p(3) = (3^2 + 2(3) + 3)\cdot \left(5(3) \:-\: \dfrac{3}{2}\right) + (3 + 2)\)
\(p(3) = 18\cdot \dfrac{27}{2} + 5\)
\(p(3) = 243 + 5\)
\(p(3) = 248\)
Soal 06
\(f(x)\) dibagi \((x^2 + 4)\) dan \((x^2 + 6)\) sisanya berturut-turut \((2x + 3)\) dan \((6x \:-\:1)\). Jika sisa pembagian \(f(x)\) oleh \((x^4 + 10x^2 + 24)\) adalah \(s(x)\), maka nilai dari \(s(4) = \dotso\)
(A) \(-109\)
(B) \(-127\)
(C) \(-129\)
(D) \(-187\)
(E) \(109\)
Jawaban:
\(f(x)\) dibagi \((x^2 + 4)\) bersisa \((2x + 3)\)
\(x^2 + 4 = 0\)
\(x^2 = -4\)
\(x = \pm \sqrt{-4} = \pm 2i\)
Catatan: \(\color{blue} \sqrt{-1} = i \text{ (imajiner) }\)
Dengan menggunakan teorema sisa dapat ditulis:
\(f(2i) = 2(2i) + 3\)
\(f(2i) = 4i + 3\dotso \color{red} (1)\)
\(f(-2i) = 2(-2i) + 3\)
\(f(-2i) = -4i + 3\dotso \color{red} (2)\)
\(f(x)\) dibagi \((x^2 + 6)\) bersisa \((6x \:-\:1)\)
\(x^2 + 6 = 0\)
\(x^2 = -6\)
\(x = \pm \sqrt{-6}\)
\(x = \pm \sqrt{6} i\)
\(f(\sqrt{6}i )= 6(\sqrt{6} i ) \:-\:1\)
\(f(\sqrt{6}i)= 6\sqrt{6} i \:-\:1\dotso \color{red} (3)\)
\(f(-\sqrt{6}i)= 6(-\sqrt{6} i ) \:-\:1\)
\(f(-\sqrt{6}i)= -6\sqrt{6} i \:-\:1 \dotso \color{red} (4)\)
\(f(x)\) dibagi oleh \((x^4 + 10x^2 + 24)\) bersisa \(s(x)\)
\(f(x) = (x^4 + 10x^2 + 24) \cdot H(x) + s(x)\)
Misal \(s(x) = ax^3 + bx^2 + cx + d\)
\(f(x) = (x^2 + 6)(x^2 + 4) \cdot H(x) + (ax^3 + bx^2 + cx + d)\)
