A. Data Tunggal
Mean (rata-rata) dari data: \(x_1, x_2, x_3, x_4, \dotso, x_n\) adalah \(\bar {x}\)
\(\bar{x} = \dfrac{\displaystyle\sum\limits_{i=1}^n x_i}{n}\)
\(\bar{x} = \dfrac{x_1 + x_2 + x_3 + x_4 + \dotso + x_n}{n}\)
\(n = \text{ banyak data}\)
B. Data Kelompok
\(\color{blue}\bar {x} = \dfrac{\sum (f_i \cdot x_i)}{\sum f_i}\)
\(\color{purple}\text{x}_i\) = titik tengah kelas = ½ × (batas atas + batas bawah)
\(\color{purple}\sum f_i\) = total frekuensi
Contoh soal
Tentukan rata-rata data di bawah ini:
| Nilai | Frekuensi |
| 3 − 7 | 2 |
| 8 − 12 | 5 |
| 13 − 17 | 4 |
| 18 − 22 | 2 |
| 23 − 27 | 6 |
| 28 − 32 | 1 |
Penyelesaian:
| Nilai | $f_i$ | $x_i$ | $f_i\cdot x_i$ |
| 3 − 7 | 2 | 5 | 10 |
| 8 − 12 | 5 | 10 | 50 |
| 13 − 17 | 4 | 15 | 60 |
| 18 − 22 | 2 | 20 | 40 |
| 23 − 27 | 6 | 25 | 150 |
| 28 − 32 | 1 | 30 | 30 |
| Total | 20 | 340 |
\(\bar {x} = \dfrac{\sum (f_i \cdot x_i)}{\sum f_i}\)
\(\bar {x} = \dfrac{340}{20}\)
\(\bar {x} = 17\)
Jadi, nilai rata-rata data di atas adalah 17
\(\color{blue} \bar {x} = \bar {x}_s + \left(\dfrac{\sum f_i \cdot u_i}{\sum f_i}\right)\cdot c\)
\(\color{purple}u_i\) = pengkodean data (data dengan frekuensi terbesar diberi kode nol)
\(\color{purple}\bar {x}_s\) = rataan sementara = titik tengah kelas yang diberi kode nol
\(\color{purple} c\) = panjang kelas
\(\color{purple}\sum f_i\) = total frekuensi
Contoh soal
Gunakan metode coding untuk menentukan nilai rata-rata data di bawah ini:
| Nilai | Frekuensi |
| 3 − 7 | 2 |
| 8 − 12 | 5 |
| 13 − 17 | 4 |
| 18 − 22 | 2 |
| 23 − 27 | 6 |
| 28 − 32 | 1 |
Penyelesaian:
| Nilai | $f_i$ | $u_i$ | $f_i\cdot u_i$ |
| 3 − 7 | 2 | −3 | −6 |
| 8 − 12 | 5 | −2 | −10 |
| 13 − 17 | 4 | −1 | −4 |
| 18 − 22 | 2 | 0 | 0 |
| 23 − 27 | 6 | 1 | 6 |
| 28 − 32 | 1 | 2 | 2 |
| Total | 20 | −12 |
\(\bar {x}_s\) adalah titik tengah kelas 18 − 22.
\(\bar {x}_s = 20\)
\(\bar {x} = \bar {x}_s + \left(\dfrac{\sum f_i \cdot u_i}{\sum f_i}\right)\cdot c\)
\(\bar {x} = 20 + \left(\dfrac{-12}{20}\right)\cdot 5\)
\(\bar {x} = 20 + \dfrac{-60}{20}\)
\(\bar {x} = 20 \:-\:3\)
\(\bar {x} = 17\)
Jadi, nilai rata-rata data di atas adalah 17
LATIHAN SOAL
Soal 01
Sekumpulan data: \(x_1, x_2, x_3, \dotso, x_{100}\) mempunyai rata-rata 44, maka rata-rata dari data: \((3x_1 + 1), (3x_2 + 4), (3x_3 + 7), \dotso, (3x_{100} + 298)\) adalah…
(A) 280,5
(B) 281,5
(C) 282,5
(D) 283,5
(E) 284,0
Jawaban: B
\(\bar{x}_{\text{baru}} = 3\cdot\bar{x}_{\text{lama}} + \dfrac{1 + 4 + 7 + \dotso + 298}{100}\)
\(\bar{x}_{\text{baru}} = 3(44) + \dfrac{1 + 4 + 7 + \dotso + 298}{100}\)
Menghitung jumlah deret aritmetika \(1 + 4 + 7 + \dotso + 298\)
\(\color{blue} s_n = \dfrac{n}{2}(a + U_n)\)
\(s_{100} = \dfrac{100}{2}(1 + 298)\)
\(s_{100} = 50(299)\)
\(s_{100} = 50(299)\)
\(s_{100} = 14.950\)
\(\bar{x}_{\text{baru}} = 3(44) + \dfrac{14.950}{100}\)
\(\bar{x}_{\text{baru}} = 132 + 149,5\)
\(\bar{x}_{\text{baru}} = 281,5\)
Soal 02
Rata-rata nilai ulangan siswa kelas XI yang jumlahnya 30 orang adalah 82. Jika nilai Adi, Budi, dan Carly tidak diikutkan maka rata-ratanya menjadi 83. Jika nilai Adi adalah 88 dan nilai Budi 91, maka nilai Carly adalah…
(A) 20
(B) 30
(C) 40
(D) 50
(E) 60
Jawaban: C
Mengitung jumlah nilai dari 30 orang siswa
\(\bar{x} = \dfrac{\text{ jumlah nilai 30 orang siswa}}{n}\)
\(82 = \dfrac{\text{ jumlah nilai 30 orang siswa}}{30}\)
\(\text{ jumlah nilai 30 orang siswa} = 82 \times 30 = 2.460\)
Mengitung jumlah nilai dari 27 orang siswa (Adi, Budi, dan Carly tidak diikutkan)
\(83 = \dfrac{\text{ jumlah nilai 27 orang siswa}}{27}\)
\(\text{ jumlah nilai 27 orang siswa} = 83 \times 27 = 2.241\)
Mengitung jumlah nilai Adi, Budi, dan Carly
Jumlah nilai Adi, Budi, dan Carly = 2.460 − 2.241 = 219
Nilai Carly = 219 − nilai Adi − nilai Budi
Nilai Carly = 219 − 88 − 91
Nilai Carly = 40
Soal 03
Rataan hitung dari data tunggal berbobot yang disajikan dalam bentuk histogram di bawah ini adalah…
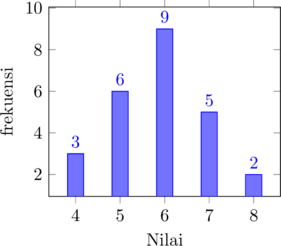
(A) 5,68
(B) 5,72
(C) 5,88
(D) 5,92
(E) 6,20
Jawaban: C
\(\bar{x} = \dfrac{\sum x_i \cdot f_i}{\sum f}\)
\(\bar{x} = \dfrac{4(3) + 5(6) + 6(9) + 7(5) + 8(2)}{3 + 6 + 9 + 5 + 2}\)
\(\bar{x} = \dfrac{12 + 30 + 54 + 35 + 16}{25}\)
\(\bar{x} = \dfrac{147}{25} = 5,88\)
Soal 04
Sebuah data terdiri dari 6 datum bernilai bulat dengan jangkauan 7, memiliki modus 12, dan median 13. Jika rata-rata maksimum yang mungkin adalah \(\bar{x}_{\text{max}}\) dan rata-rata minimum yang mungkin adalah \(\bar{x}_{\text{min}}\), maka nilai \(\bar{x}_{\text{max}}\:-\:\bar{x}_{\text{min}} = \dotso\)
(A) \(\dfrac{4}{3}\)
(B) \(\dfrac{5}{3}\)
(C) \(\dfrac{6}{3}\)
(D) \(\dfrac{7}{3}\)
(E) \(\dfrac{8}{3}\)
Jawaban: B
Kemungkinan 1:
Untuk mendapatkan rata-rata maksimum maka datanya adalah:
\(12, 12, 12, 14, 19, 19\)
\(\bar{x}_{\text{max}} = \dfrac{12 + 12 + 12 + 14 + 19 + 19}{6} = \dfrac{88}{6}\)
Kemungkinan 2:
Untuk mendapatkan rata-rata minimum maka datanya adalah:
\(9, 12, 12, 14, 15, 16\)
\(\bar{x}_{\text{min}} = \dfrac{9 + 12 + 12 + 14 + 15 + 16}{6} = \dfrac{78}{6}\)
\(\bar{x}_{\text{max}}\:-\:\bar{x}_{\text{min}} = \dfrac{88}{6}\:-\: \dfrac{78}{6} = \dfrac{10}{6} = \dfrac{5}{3}\)
Soal 05
Perhatikan histogram di bawah ini:

Rataan hitung data di atas adalah…
(A) 36,5
(B) 37,0
(C) 37,5
(D) 38,0
(E) 38,5
Jawaban: A
Menghitung mean (rata-rata) dengan metode coding
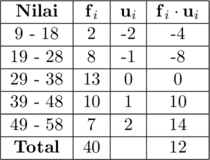
\(\bar{\text{x}} = \text{x}_{\text{s}} + \left(\dfrac{\sum \text{f}_i \cdot \text{u}_i}{\sum \text{f}_i}\right)\cdot \text{c}\)
\(\text{u}_i\) adalah pengkodean (data dengan frekuensi terbesar diberi kode nol)
\(\text{x}_{\text{s}}\) adalah rataan sementara = titik tengah kelas yang diberi kode nol, yaitu \(\dfrac{29 + 38}{2} = \color{blue}33,5\)
\(\text{c}\) adalah panjang kelas, yaitu \(38,5 \:-\:28,5 = \color{blue} 10\)
\(\sum\text{f}_i\) adalah total frekuensi, yaitu \(\color{blue} 40\)
\(\bar{\text{x}} = 33,5 + \dfrac{12}{40}\cdot 10\)
\(\bar{\text{x}} = 33,5 + \dfrac{120}{40}\)
\(\bar{\text{x}} = 33,5 + 3\)
\(\bar{\text{x}} = 36,5\)
Jadi mean (rata-rata) data tersebut adalah 36,5
Soal 06
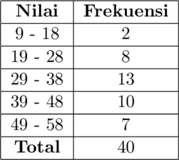
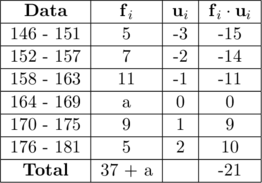
Jika rataan hitung dari data di bawah adalah 164,25, maka nilai \(a\) adalah…
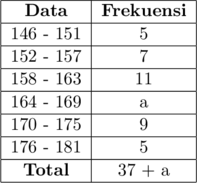
(A) 17
(B) 19
(C) 21
(D) 23
(E) 25
Jawaban: B
\(\bar{\text{x}} = \text{x}_{\text{s}} + \left(\dfrac{\sum \text{f}_i \cdot \text{u}_i}{\sum \text{f}_i}\right)\cdot \text{c}\)
\(\text{u}_i\) adalah pengkodean (data dengan frekuensi terbesar diberi kode nol)
\(\text{x}_{\text{s}}\) adalah rataan sementara = titik tengah kelas yang diberi kode nol, yaitu \(\dfrac{164 + 169}{2} = \color{blue} 166,5\)
\(\text{c}\) adalah panjang kelas, yaitu \(169,5 \:-\:163,5 = \color{blue} 6\)
\(\sum\text{f}_i\) adalah total frekuensi, yaitu \(\color{blue}37 + a\)
\(\bar{\text{x}} = 166,5 + \dfrac{-21}{37 + a}\cdot 6\)
\(164,25 = 166,5 + \dfrac{-126}{37 + a}\)
\(-2,25 = \dfrac{-126}{37 + a}\)
\(2,25(37 + a) = 126\)
\(83,25 + 2,25a = 126\)
\(2,25a = 42,75\)
\(a = \dfrac{42,75}{2,25}\)
\(a = 19\)
Soal 07
Di bawah ini data umur pasien yang datang ke puskesmas hari ini.
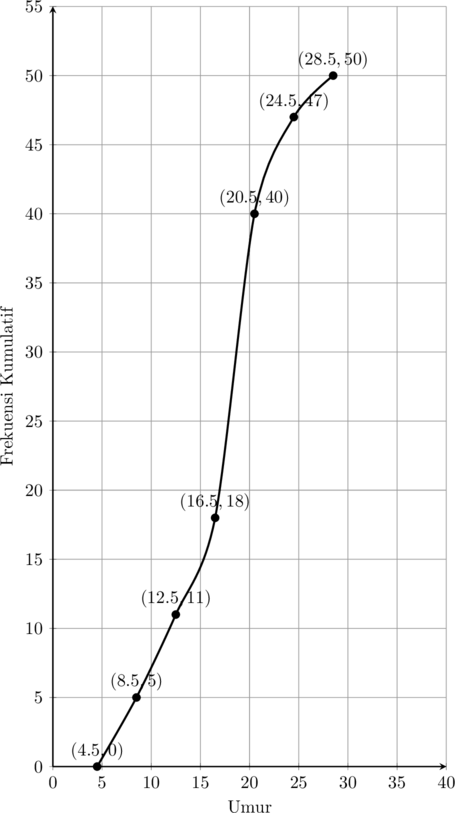
Rataan hitung data di atas adalah…
(A) 15,66
(B) 16,66
(C) 16,74
(D) 16,82
(E) 16,94
Jawaban: D
Ogive positif merupakan grafik yang diperoleh dari tabel distribusi frekuensi kumulatif kurang dari.
- Data yang kurang dari atau sama dengan 8,5 ada sebanyak 5
- Data yang kurang dari atau sama dengan 12,5 ada sebanyak 11 − 5 = 6
- Data yang kurang dari atau sama dengan 16,5 ada sebanyak 18 − 11 = 7
- Data yang kurang dari atau sama dengan 20,5 ada sebanyak 40 − 18 = 22
- Data yang kurang dari atau sama dengan 24,5 ada sebanyak 47 − 40 = 7
- Data yang kurang dari atau sama dengan 28,5 ada sebanyak 50 − 47 = 3
Tabel distribusi frekuensi kumulatif kurang dari tepi atas kelas dapat dibuat sebagai berikut:
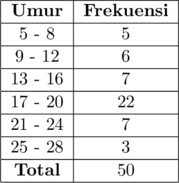
Menghitung mean (rata-rata) dengan metode coding
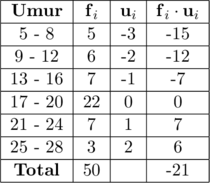
\(\bar{\text{x}} = \text{x}_{\text{s}} + \left(\dfrac{\sum \text{f}_i \cdot \text{u}_i}{\sum \text{f}_i}\right)\cdot \text{c}\)
\(\text{u}_i\) adalah pengkodean (data dengan frekuensi terbesar diberi kode nol)
\(\text{x}_{\text{s}}\) adalah rataan sementara = titik tengah kelas yang diberi kode nol, yaitu \(\dfrac{17 + 20}{2} = \color{blue} 18,5\)
\(\text{c}\) adalah panjang kelas, yaitu \(20,5 \:-\:16,5 = \color{blue} 4\)
\(\sum\text{f}_i\) adalah total frekuensi, yaitu \(\color{blue} 50\)
\(\bar{\text{x}} = 18,5 + \dfrac{-21}{50}\cdot 4\)
\(\bar{\text{x}} = 18,5 + \dfrac{-84}{50}\)
\(\bar{\text{x}} = 18,5 \:-\: 1,68\)
\(\bar{\text{x}} = 16,82\)
Jadi mean (rata-rata) data tersebut adalah 16,82
