Berikut ini adalah kurva ogive positif dari suatu data kelompok.
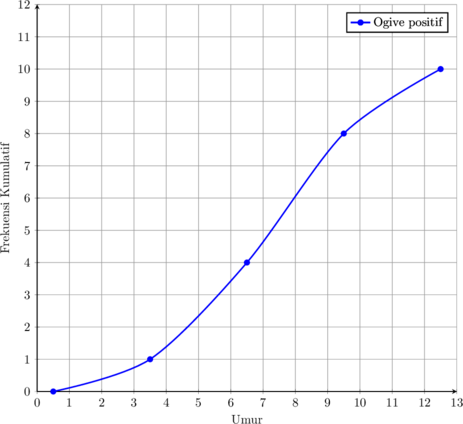
Dari kurva di atas, tentukan:
(1) Kuartil bawah
(2) Kuartil tengah (median)
(3) Kuartil atas
(4) Simpangan kuartil
(5) Mean
(6) Modus
(7) Variansi
(8) Simpangan baku
PEMBAHASAN
Ogive positif merupakan grafik yang diperoleh dari tabel distribusi frekuensi kumulatif kurang dari.
- Data yang kurang dari atau sama dengan 3,5 ada sebanyak 1
- Data yang kurang dari atau sama dengan 6,5 ada sebanyak 4 − 1 = 3
- Data yang kurang dari atau sama dengan 9,5 ada sebanyak 8 − 4 = 4
- Data yang kurang dari atau sama dengan 12,5 ada sebanyak 10 − 8 = 2
Tabel distribusi frekuensi kumulatif kurang dari tepi atas kelas dapat dibuat sebagai berikut:
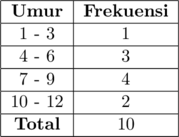
(1) Menghitung Kuartil Bawah (\(\text{Q}_1\))
Kelas kuartil 1 berada di data ke \(\frac{1}{4}\cdot 10 = 2,5\), yaitu \(\color{blue} (4 \:-\: 6)\)
\(\color{purple}\text{Q}_1 = \text{tb} + \dfrac{\left(\frac{1}{4}\text{n}\:-\:\sum \text{Fk}\right)}{\text{f}}\cdot \text{c}\)
\(\text{tb}\) adalah tepi bawah kelas kuartil bawah, yaitu \(4\:-\:0,5 = \color{blue} 3,5\)
\(\text{Fk}\) adalah frekuensi kumulatif sebelum kelas kuartil bawah, yaitu \(\color{blue} 1\)
\(\text{f}\) adalah frekuensi kelas kuartil bawah, yaitu \(\color{blue} 3\)
\(\text{c}\) adalah panjang kelas = tepi atas kelas − tepi bawah kelas, yaitu \(6,5 \:-\: 3,5 = \color{blue} 3\)
\(\color{purple}\text{Q}_1 = 3,5 + \dfrac{(2,5\:-\:1)}{3}\cdot 3\)
\(\color{purple}\text{Q}_1 = 3,5 + \dfrac{1,5}{\cancel{3}}\cdot \cancel{3}\)
\(\color{purple}\text{Q}_1 = 3,5 + 1,5\)
\(\color{purple}\text{Q}_1 = 5\)
Jadi, kuartil bawahnya adalah 5
(2) Menghitung Kuartil Tengah (\(\text{Q}_2\))
Kelas kuartil 2 berada di data ke \(\frac{1}{2}\cdot 10 = 5\), yaitu \(\color{blue} (7 \:-\: 9)\)
\(\color{purple}\text{Q}_2 = \text{tb} + \dfrac{\left(\frac{1}{2}\text{n}\:-\:\sum \text{Fk}\right)}{\text{f}}\cdot \text{c}\)
\(\text{tb}\) adalah tepi bawah kelas kuartil tengah, yaitu \(7\:-\:0,5 = \color{blue} 6,5\)
\(\text{Fk}\) adalah frekuensi kumulatif sebelum kelas kuartil tengah, yaitu \(1 + 3 = \color{blue} 4\)
\(\text{f}\) adalah frekuensi kelas kuartil tengah, yaitu \(\color{blue} 4\)
\(\text{c}\) adalah panjang kelas = tepi atas kelas − tepi bawah kelas, yaitu \(9,5 \:-\: 6,5 = \color{blue} 3\)
\(\color{purple}\text{Q}_2 = 6,5 + \dfrac{(5\:-\:4)}{4}\cdot 3\)
\(\color{purple}\text{Q}_2 = 6,5 + \frac{3}{4}\)
\(\color{purple}\text{Q}_2 = 6,5 + 0,75\)
\(\color{purple}\text{Q}_2 = 7,25\)
Jadi, kuartil tengahnya adalah 7,25
(3) Menghitung Kuartil Atas (\(\text{Q}_3\))
Kelas kuartil 3 berada di data ke \(\frac{3}{4}\cdot 10 = 7,5\), yaitu \(\color{blue} (7 \:-\: 9)\)
\(\color{purple}\text{Q}_3 = \text{tb} + \dfrac{\left(\frac{3}{4}\text{n}\:-\:\sum \text{Fk}\right)}{\text{f}}\cdot \text{c}\)
\(\text{tb}\) adalah tepi bawah kelas kuartil atas, yaitu \(7\:-\:0,5 = \color{blue} 6,5\)
\(\text{Fk}\) adalah frekuensi kumulatif sebelum kelas kuartil atas, yaitu \(1 + 3 = \color{blue} 4\)
\(\text{f}\) adalah frekuensi kelas kuartil atas, yaitu \(\color{blue} 4\)
\(\text{c}\) adalah panjang kelas = tepi atas kelas − tepi bawah kelas, yaitu \(9,5 \:-\: 6,5 = \color{blue} 3\)
\(\color{purple}\text{Q}_3 = 7,5 + \dfrac{(7,5\:-\:4)}{4}\cdot 3\)
\(\color{purple}\text{Q}_3= 7,5 + \frac{10,5}{4}\)
\(\color{purple}\text{Q}_3 = 7,5 + 2,625\)
\(\color{purple}\text{Q}_3 = 10,125\)
Jadi, kuartil atasnya adalah 10,125
(4) Menghitung Simpangan Kuartil
\(\text {Simpangan kuartil} = \frac{1}{2}(\text{Q}_3\:-\:\text{Q}_1)\)
\(\text {Simpangan kuartil} = \frac{1}{2}(10,125\:-\:5)\)
\(\text {Simpangan kuartil} = \frac{1}{2}(5,125)\)
\(\text {Simpangan kuartil} = 2,5625\)
(5) Menghitung Mean
Menghitung mean (rata-rata) dengan metode coding
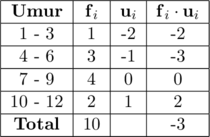
\(\bar{\text{x}} = \text{x}_{\text{s}} + \left(\dfrac{\sum \text{f}_i \cdot \text{u}_i}{\sum \text{f}_i}\right)\cdot \text{c}\)
\(\text{u}_i\) adalah pengkodean (data dengan frekuensi terbesar diberi kode nol)
\(\text{x}_{\text{s}}\) adalah rataan sementara = titik tengah kelas yang diberi kode nol, yaitu \(\dfrac{7 + 8}{2} = \color{blue} 8\)
\(\text{c}\) adalah panjang kelas, yaitu \(9,5 \:-\:6,5 = \color{blue} 3\)
\(\sum\text{f}_i\) adalah total frekuensi, yaitu \(\color{blue} 10\)
\(\bar{\text{x}} = 8 + \frac{-3}{10}\cdot 3\)
\(\bar{\text{x}} = 8 + \frac{-9}{10}\)
\(\bar{\text{x}} = 8 \:-\: 0,9\)
\(\bar{\text{x}} = 7,1\)
Jadi mean (rata-rata) data tersebut adalah 7,1
(6) Menghitung Modus
Modus berada di kelas dengan frekuensi terbesar, yaitu \(7\:-\:9\)
\(\text{Modus} = \text{tb} + \left(\dfrac{\text{d}_1}{\text{d}_1 + \text{d}_2}\right)\cdot \text{c}\)
\(\text{tb}\) adalah tepi bawah kelas modus, yaitu \(7\:-\:0,5 = \color{blue} 6,5\)
\(\text{d}_1\) adalah selisih frekuensi kelas modus dengan kelas sebelumnya, yaitu \(4\:-\:3 = \color{blue} 1\)
\(\text{d}_2\) adalah selisih frekuensi kelas modus dengan kelas setelahnya, yaitu \(4\:-\:2 = \color{blue} 2\)
\(\text{Modus} = 6,5 + \left(\dfrac{1}{1 + 2}\right)\cdot 3\)
\(\text{Modus} = 6,5 + \left(\dfrac{1}{\cancel{3}}\right)\cdot \cancel{3}\)
\(\text{Modus} = 6,5 + 1\)
\(\text{Modus} = 7,5\)
Jadi, modus data tersebut adalah 7,5
(7) Menghitung Variansi
Menghitung variansi (ragam) dengan metode coding
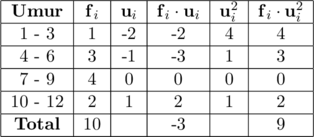
\(\text{s}^2 = \left[\dfrac{\sum \text{f}_i\cdot \text{u}^2_i}{\sum \text {f}_i}\:-\: \left(\dfrac{\sum \text{f}_i \cdot \text{u}_i}{\sum \text{f}_i}\right)^2\right]\cdot \text{c}^2\)
\(\text{s}^2 = \left[\dfrac{9}{10}\:-\: \left(\dfrac{-3}{10}\right)^2\right]\cdot 3^2\)
\(\text{s}^2 = \left[\dfrac{9}{10}\:-\: \dfrac{9}{100}\right]\cdot 9\)
\(\text{s}^2 = \dfrac{81}{100}\cdot 9\)
\(\text{s}^2 = \dfrac{729}{100}\)
\(\text{s}^2 = 7,29\)
Jadi variansi data tersebut adalah 7,29
(8) Menghitung Simpangan Baku
\(\text{Simpangan baku} = \sqrt{\text{variansi}}\)
\(\text{Simpangan baku} = \sqrt{\dfrac{729}{100}}\)
\(\text{Simpangan baku} = \frac{27}{10} = 2,7\)
