Soal 01
Diberikan pernyataan yang berkaitan dengan tabel distribusi frekuensi di bawah ini
| Nilai | Frekuensi |
| 1,0 – 2,1 | 2 |
| 2,2 – 3,3 | 7 |
| 3,4 – 4,5 | 15 |
| 4,6 – 5,7 | 20 |
| 5,8 – 6,9 | 3 |
| 7,0 – 8,1 | 1 |
(1) Tepi atas kelas yang memuat modus adalah 5,75
(2) Kelas yang memuat kuartil atas adalah kelas keempat
(3) Lebar kelas adalah 1,1
(4) Titik tengah kelas kelima adalah 6,35
(5) Jangkauan data adalah 6
(6) Batas bawah kelas keenam adalah 5,75
Banyaknya pernyataan yang benar adalah…
(A) 1
(B) 2
(C) 3
(D) 4
(E) 5
Jawaban: D
(1) Tepi atas kelas yang memuat modus adalah 5,75 (Benar)
Modus berada di kelas yang memiliki frekuensi terbesar yaitu kelas keempat (4,6 – 5,7)
Batas bawah kelas modus = 4,6
Batas atas kelas modus = 5,7
Tepi atas kelas modus = (batas atas kelas keempat + batas bawah kelas kelima) ÷ 2
Tepi atas kelas modus = (5,7 + 5,8) ÷ 2
Tepi atas kelas modus = 5,75
(2) Kelas yang memuat kuartil atas adalah kelas keempat (Benar)
Kuartil atas disebut juga \(\text{Q}_3\)
Total frekuensi \(n = 48\)
\(\text{Q}_3\) terletak di \(x_{\frac{3}{4}\cdot n} = x_{\frac{3}{4}\cdot 48} = x_{36} \)
Data ke-36 terletak di kelas keempat (4,6 – 5,7)
(3) Lebar kelas adalah 1,1 (Salah)
Lebar kelas = tepi atas kelas − tepi bawah kelas
Misal kita ambil kelas kedua (2,2 − 3,3)
Tepi atas kelas kedua = (batas atas kelas kedua + batas bawah kelas ketiga) ÷ 2
Tepi atas kelas kedua = (3,3 + 3,4) ÷ 2
Tepi atas kelas kedua = 3,35
Tepi bawah kelas kedua = (batas bawah kelas kedua + batas atas kelas pertama) ÷ 2
Tepi bawah kelas kedua = (2,2 + 2,1) ÷ 2
Tepi bawah kelas kedua = 2,15
Lebar kelas = tepi atas kelas − tepi bawah kelas
Lebar kelas = 3,35 − 2,15 = 1,2
Jadi, lebar kelas seharusnya adalah 1,2
(4) Titik tengah kelas kelima adalah 6,35 (Benar)
Kelas kelima adalah 5,8 – 6,9
Titik tengah kelas kelima = (batas bawah kelas + batas atas kelas) ÷ 2
Titik tengah kelas kelima = (5,8 + 6,9) ÷ 2
Titik tengah kelas kelima = 6,35
(5) Jangkauan data adalah 6 (Benar)
Jangkauan (range) = titik tengah kelas terakhir − titik tengah kelas pertama
Jangkauan (range) = titik tengah kelas keenam − titik tengah kelas pertama
Jangkauan (range) = \(\dfrac{7,0 + 8,1}{2}\:-\:\dfrac{1,0 + 2,1}{2}\)
Jangkauan (range) = \(7,55\:-\:1,55 = 6\)
(6) Batas bawah kelas keenam adalah 5,75 (Salah)
Kelas keenam adalah 5,8 – 6,9
Batas atas kelas keenam = 6,9
Batas bawah kelas keenam seharusnya adalah 5,8
Soal 02
Diberikan ogive negatif dan tabel distribusi frekuensi dan tabel distribusi frekuensi kumulatif.
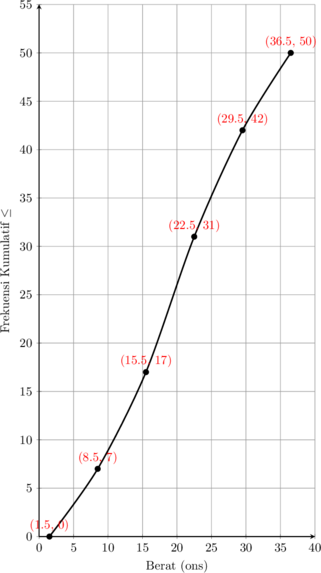
(1) Tepi atas kelas pertama adalah 8,5
(2) Batas bawah kelas kedua adalah 9
(3) Frekuensi kelas ketiga adalah 14
(4) Panjang kelasnya adalah 7
(5) Jangkauannya adalah 29
Banyaknya pernyataan yang benar adalah…
(A) 1
(B) 2
(C) 3
(D) 4
(E) 5
Jawaban: D
Ogive disebut juga poligon frekuensi kumulatif. Untuk ogive positif menunjukkan frekuensi kumulatif kurang dari atau sama dengan tepi atas masing-masing kelas. Ogive positif memiliki ciri kurva yang selalu naik.
| Berat (ons) | frekuensi |
| 2 − 8 | 7 |
| 9 − 15 | 10 |
| 16 − 22 | 14 |
| 23 − 29 | 11 |
| 30 − 36 | 8 |
(1) Tepi atas kelas pertama adalah 8,5 (Benar)
Kelas pertama adalah 2 − 8
Tepi atas kelas pertama = (batas atas kelas pertama + batas bawah kelas kedua) ÷ 2
Tepi atas kelas pertama = (8 + 9) ÷ 2 = 8,5
(2) Batas bawah kelas kedua adalah 9 (Benar)
Kelas kedua adalah 9 − 15
Batas atas kelas kedua = 15
Batas bawah kelas kedua = 9
(3) Frekuensi kelas ketiga adalah 14 (Benar)
Kelas ketiga adalah 16 − 22, memiliki frekuensi 14
(4) Panjang kelasnya adalah 7 (Benar)
Panjang kelas = tepi atas kelas − tepi bawah kelas
Misal pada kelas pertama (2 − 8)
Panjang kelas = 8,5 − 1,5 = 7
(5) Jangkauannya adalah 29 (Salah)
Jangkauan = titik tengah kelas terakhir − titik tengah kelas pertama
Jangkauan = \(\dfrac{30 + 36}{2} \:-\: \dfrac{2 + 8}{2}\)
Jangkauan = \(33\:-\:5 = 28\)
Jangkauan data seharusnya adalah 28
Soal 03
Di bawah ini adalah data nilai ujian matematika dari 120 orang siswa kelas 12. Jika hanya ada 20 siswa yang lulus ujian, maka batas nilainya adalah…
| Nilai | Frekuensi |
| 11 − 25 | 15 |
| 26 − 40 | 30 |
| 41 − 55 | 40 |
| 56 − 70 | 20 |
| 71 − 85 | 12 |
| 86 − 100 | 3 |
| Total | 120 |
(A) > 50,75
(B) > 55,25
(C) > 56,78
(D) > 66,75
(E) > 70,50
Jawaban: D
Jumlah siswa yang lulus = 20 orang
Jumlah siswa yang tidak lulus (N) = 120 − 20 = 100 orang
\(\color{blue}\text{Batas nilai} > \text{tb} + \left(\dfrac{\text{N}\:-\:\sum \text{Fk}}{\text{f}}\right)\cdot \text {c}\)
Note:
\(\text{tb} = \text{ tepi bawah kelas yang memuat batas nilai}\)
\(\text{N} = \text{ jumlah siswa yang tidak lulus ujian}\)
\(\sum \text{Fk} = \text{ frekuensi kumulatif sebelum kelas yang memuat batas nilai}\)
\(\text{f} = \text{ frekuensi kelas yang memuat batas nilai}\)
\(\text{c} = \text{ panjang kelas}\)
Dengan jumlah siswa yang tidak lulus ujian sebanyak 100 orang, maka batas nilai terletak di kelas 56 − 70.
\(\text{Batas nilai} > \text{tb} + \left(\dfrac{\text{N}\:-\:\sum \text{Fk}}{\text{f}}\right)\cdot \text {c}\)
\(\text{Batas nilai} > 55,5 + \left(\dfrac{100\:-\:85}{20}\right)\cdot 15\)
\(\text{Batas nilai} > 55,5 + \left(\dfrac{15}{20}\right)\cdot 15\)
\(\text{Batas nilai} > 55,5 + 11,25\)
\(\text{Batas nilai} > 66,75\)
Jadi, batas nilai untuk dapat lulus ujian matematika adalah > 66,75
Soal 04
Perhatikan data berikut:
| Nilai | Frekuensi |
| 10 – 14 | 2 |
| 15 – 19 | 4 |
| 20 – 24 | 5 |
| 25 – 29 | 6 |
| 30 – 34 | 3 |
Simpangan rata-rata data di atas adalah…
(A) 2,1
(B) 3,2
(C) 4,3
(D) 4,5
(E) 5,1
Jawaban: E
| Nilai | \(f_i\) | Titik tengah kelas \((x_i)\) | \(f_i \cdot x_i\) |
| 10 – 14 | 2 | 12 | 24 |
| 15 – 19 | 4 | 17 | 68 |
| 20 – 24 | 5 | 22 | 110 |
| 25 – 29 | 6 | 27 | 162 |
| 30 – 34 | 3 | 32 | 96 |
| Total | 20 | 460 |
Menghitung rata-rata \(\bar {x}\)
\(\bar{ x} = \dfrac{\sum f_i \cdot x_i}{\sum f_i}\)
\(\bar {x} = \dfrac{460}{20} = 23\)
Simpangan rata-rata (SR)
\(\text{SR} = \dfrac{\sum f_i \cdot |x_i\:-\:\bar{x}|}{\sum f_i}\)
\(\text{SR} = \dfrac{2|12\:-\:23| + 4|17\:-\:23| + 5|22\:-\:23| + 6|27\:-\:23| + 3|32\:-\:23|}{20}\)
\(\text{SR} = \dfrac{2(11) + 4(6)+ 5(1) + 6(4) + 3(9)}{20}\)
\(\text{SR} = \dfrac{22 + 24 + 5 + 24 + 27}{20}\)
\(\text{SR} = \dfrac{102}{20}\)
\(\text{SR} = 5,1\)
Soal 05
Perhatikan data berikut:
| Nilai | Frekuensi |
| 5 – 7 | 3 |
| 8 – 10 | 4 |
| 11 – 13 | 7 |
| 14 – 16 | 3 |
| 17 – 19 | 2 |
| 20 – 22 | 1 |
Variansi data di atas adalah…
(A) 16,0
(B) 16,1
(C) 16,2
(D) 17,1
(E) 17,2
Jawaban: C
| Nilai | \(f_i\) | \(x_i\) | \(u_i\) | \(f_i\cdot u_i\) | \(u^2_i\) | \(f_i \cdot u^2_i\) |
| 5 – 7 | 3 | 6 | -3 | -9 | 9 | 27 |
| 8 – 10 | 4 | 9 | -2 | -8 | 4 | 16 |
| 11 – 13 | 7 | 12 | -1 | -7 | 1 | 7 |
| 14 – 16 | 3 | 15 | 0 | 0 | 0 | 0 |
| 17 – 19 | 2 | 18 | +1 | 2 | 1 | 2 |
| 20 – 22 | 1 | 21 | +2 | 2 | 4 | 4 |
| Total | 20 | -20 | 56 |
Menghitung variansi \(s^2\)
\(\color{blue} s^2 = \left[\dfrac{\sum f_i \cdot u^2_i}{n}\:-\:\left(\dfrac{\sum f_i \cdot x_i}{n} \right)^2\right]\cdot c^2\)
\(s^2 = \left[\dfrac{56}{20}\:-\:\left(\dfrac{-20}{20} \right)^2\right]\cdot 3^2\)
\(s^2 = \left[2,8\:-\:1\right]\cdot 9\)
\(s^2 = 1,8\cdot 9\)
\(s^2 = 16,2\)
Jadi, nilai variansi data di atas adalah 16,2
Soal 06
Perhatikan data berikut:
| Nilai | Frekuensi |
| 2 – 8 | 1 |
| 9 – 15 | 2 |
| 16 – 22 | 5 |
| 23 – 29 | 7 |
| 30 – 36 | 2 |
| 37 – 43 | 3 |
Terdapat pernyataan-pernyataan terkait data di atas
(1) Rata-rata data = 24,6
(2) Kuartil bawah = 18,3
(3) Median = 24,5
(4) Kuartil atas = 29,5
(5) Modus = 24,5
Pernyataan yang bernilai benar ada sebanyak…
(A) 1
(B) 2
(C) 3
(D) 4
(E) 5
Jawaban: E
| Nilai | \(f_i\) | \(u_i\) | \(f_i \cdot u_i\) |
| 2 – 8 | 1 | -3 | -3 |
| 9 – 15 | 2 | -2 | -4 |
| 16 – 22 | 5 | -1 | -5 |
| 23 – 29 | 7 | 0 | 0 |
| 30 – 36 | 2 | +1 | 2 |
| 37 – 43 | 3 | +2 | 6 |
(1) Menghitung rata-rata dengan metode coding
\(\color{blue} \bar {x} = \bar {x}_{s} + \left(\dfrac{\sum f_i \cdot u_i}{\sum f_i} \right) \cdot c\)
\(\bar{x}_{s}\) disebut rata-rata sementara, merupakan titik tengah kelas yang diberi kode nol.
\(\bar {x} = \dfrac{23 + 29}{2} + \left(\dfrac{-4}{20} \right) \cdot 7\)
\(\bar {x} = 26 + \left(\dfrac{-1}{5} \right) \cdot 7\)
\(\bar {x} = 26 \:-\:1,4\)
\(\bar {x} = 24,6\)
Jadi, nilai rata-rata datanya adalah 24,6
(2) Menghitung kuartil bawah
Kuartil bawah merupakan \(x_{\frac{1}{4}\cdot n} = x_{\frac{1}{4} \cdot 20} = x_{5}\)
Data ke-5 terletak di kelas 16 – 22
\(\color{blue} Q_1 = tb + \left( \dfrac{\frac{1}{4}n \:-\:\sum F_k}{f} \right) \cdot c\)
\(\sum F_k\) merupakan frekuensi kumulatif sebelum kelas kuartil bawah.
\(\sum F_k = 1 + 2 = 3\)
\(Q_1 =15,5 + \left( \dfrac{5 \:-\:3}{5} \right) \cdot 7\)
\(Q_1 =15,5 + 2,8\)
\(Q_1 = 18,3\)
Jadi, kuartil bawah datanya adalah 18,3
(3) Menghitung median (kuartil tengah)
Median merupakan \(x_{\frac{1}{2}\cdot n} = x_{\frac{1}{2} \cdot 20} = x_{10}\)
Data ke-10 terletak di kelas 23 – 29
\(\color{blue} Q_2 = tb + \left( \dfrac{\frac{1}{2}n \:-\:\sum F_k}{f} \right) \cdot c\)
\(\sum F_k\) merupakan frekuensi kumulatif sebelum kelas median
\(\sum F_k = 1 + 2 + 5 = 8\)
\(Q_2= 22,5 + \left( \dfrac{10 \:-\:8}{7} \right) \cdot 7\)
\(Q_2 = 22,5 + 2\)
\(Q_2= 24,5\)
Jadi, median datanya adalah 24,5
(4) Menghitung kuartil atas
Kuartil atas merupakan \(x_{\frac{3}{4}\cdot n} = x_{\frac{3}{4} \cdot 20} = x_{15}\)
Data ke-15 terletak di kelas 23 – 29
\(\color{blue} Q_3 = tb + \left( \dfrac{\frac{3}{4}n \:-\:\sum F_k}{f} \right) \cdot c\)
\(\sum F_k\) merupakan frekuensi kumulatif sebelum kelas kuartil atas
\(\sum F_k = 1 + 2 + 5 = 8\)
\(Q_3= 22,5 + \left( \dfrac{15 \:-\:8}{7} \right) \cdot 7\)
\(Q_3 = 22,5 + 7\)
\(Q_3 = 29,5\)
Jadi, kuartil atas datanya adalah 29,5
(5) Menghitung modus
Modus terletak di kelas dengan frekuensi terbesar.
Kelas modus adalah 23 – 29
\(\color{blue} \text{Mo} = tb + \left(\dfrac{d_1}{d_1 + d_2}\right) \cdot c\)
\(d_1\) = selisih frekuensi kelas modus dengan kelas sebelumnya = 7 – 5 = 2
\(d_2\) = selisih frekuensi kelas modus dengan kelas sesudahnya = 7 – 2 = 5
\(\text{Mo} = 22,5 + \left(\dfrac{2}{2 + 5}\right) \cdot 7\)
\(\text{Mo} = 22,5 + 2\)
\(\text{Mo} = 24,5 \)
Jadi, modus datanya adalah 24,5
