Soal 1
Berikut ini merupakan pernyataan tentang tabung tertutup
- Tabung termasuk bangun ruang sisi lengkung
- Tabung memiliki 3 buah rusuk
- Tabung tidak memiliki titik sudut
- Selimut tabung berbentuk lingkaran
- Alas dan atap tabung tidak sama bentuknya
- Luas alas tabung sama dengan luas lingkaran
- Tabung memiliki 2 sisi datar dan 1 sisi lengkung
Pernyatan yang benar tentang tabung adalah nomor …
(A) 1, 2, 3, 6, 7
(B) 1, 3, 5, 6, 7
(C) 1, 3, 6, 7
(D) 2, 3, 4, 5
Jawaban: C
- Tabung termasuk bangun ruang sisi lengkung
- Tabung memiliki 2 buah rusuk
- Tabung tidak memiliki titik sudut
- Selimut tabung berbentuk persegi panjang
- Alas dan atap tabung berbentuk sama yaitu lingkaran
- Luas alas tabung sama dengan luas lingkaran
- Tabung memiliki 2 sisi datar dan 1 sisi lengkung
Soal 2
Sebuah tabung memiliki luas alas 45 cm² dan tinggi 10 cm. Volume tabung tersebut adalah …
(A) 300 cm³
(B) 380 cm³
(C) 400 cm³
(D) 450 cm³
Jawaban: D
Volume tabung = luas alas × tinggi
Volume tabung = 45 cm² × 10 cm
Volume tabung = 450 cm³
Soal 3
Joni memiliki sebuah gelas kaca yang berbentuk tabung dengan ukuran diameter alas 8 cm dan tinggi 14 cm. Volume gelas kaca miliki Joni adalah …
(A) 700 cm³
(B) 704 cm³
(C) 705 cm³
(D) 708 cm³
Jawaban: B
Jari-jari tabung = \(\dfrac{1}{2}\times \text{ diameter}\)
Jari-jari tabung = \(\dfrac{1}{2}\times 8 = 4 \text{ cm}\)
Volume tabung = \(\pi \text{r}^2 \text{t}\)
Volume tabung = \(\dfrac{22}{7}\cdot 4^2 \cdot 14\)
Volume tabung = \(\dfrac{22}{\cancel{7}}\cdot 16 \cdot \cancelto{2}{14}\)
Volume tabung = 704 cm³
Soal 4
Joni memiliki sebuah gelas kaca yang berbentuk tabung dengan ukuran diameter alas 8 cm dan tinggi 14 cm. Joni mengisi \(\dfrac{3}{4}\) bagian gelasnya dengan air. Volume air yang dituangkan oleh Joni adalah … ml
(A) 528
(B) 529
(C) 532
(D) 545
Jawaban: A
Jari-jari tabung = \(\dfrac{1}{2}\times \text{ diameter}\)
Jari-jari tabung = \(\dfrac{1}{2}\times 8 = 4 \text{ cm}\)
Volume air = \(\dfrac{3}{4}\times \text{ volume tabung}\)
Volume air = \(\dfrac{3}{4}\times \pi \text{r}^2 \text{t}\)
Volume air = \(\dfrac{3}{4}\times \dfrac{22}{7}\cdot 4^2 \cdot 14\)
Volume air = \(\dfrac{3}{\cancel{4}}\times \dfrac{22}{\cancel{7}}\cdot \cancelto{4}{16} \cdot \cancelto{2}{14}\)
Volume air = 528 cm³ = 528 ml
Soal 5
Anton memiliki dua buah gelas kaca berbentuk tabung yang berwarna biru dan merah. Gelas biru memiliki ukuran jari-jari alas 7 cm, sedangkan gelas merah memiliki ukuran jari-jari alas 14 cm. Jika tinggi kedua gelas tersebut sama maka perbandingan volume gelas biru dengan gelas merah adalah …
(A) 1 : 3
(B) 1 : 4
(C) 2 : 3
(D) 7 : 14
Jawaban: B
Misalkan:
Volume gelas biru adalah \(\textbf{V}_{\text{1}}\)
Volume gelas merah adalah \(\textbf{V}_{\text{2}}\)
\(\dfrac{\textbf{V}_{\text{1}}}{\textbf{V}_{\text{2}}} = \dfrac{\pi \text{r}^2_1 \text{t}}{\pi \text{r}^2_2 \text{t}}\)
\(\dfrac{\textbf{V}_{\text{1}}}{\textbf{V}_{\text{2}}} = \dfrac{\cancel{\pi} \text{r}^2_1 \cancel{\text{t}}}{\cancel{\pi} \text{r}^2_2 \cancel{\text{t}}}\)
\(\dfrac{\textbf{V}_{\text{1}}}{\textbf{V}_{\text{2}}} = \dfrac{\text{r}^2_1}{\text{r}^2_2}\)
\(\dfrac{\textbf{V}_{\text{1}}}{\textbf{V}_{\text{2}}} = \dfrac{7^2}{14^2}\)
\(\dfrac{\textbf{V}_{\text{1}}}{\textbf{V}_{\text{2}}} = \dfrac{49}{196}\)
\(\dfrac{\textbf{V}_{\text{1}}}{\textbf{V}_{\text{2}}} = \dfrac{1}{4}\)
\(\textbf{V}_{\text{1}} : \textbf{V}_{\text{2}} = 1 : 4\)
Jadi perbandingan volume gelas biru dengan gelas merah adalah 1 : 4
Soal 6
Sebuah gelas kaca berbentuk tabung memiliki tinggi 24 cm dan jari-jari alas 10 cm. Jika \(\dfrac{3}{4}\) bagian gelas tersebut sudah terisi air, maka berapa banyak air yang harus ditambahkan agar gelas menjadi penuh dengan air?
(A) \(1.878 \text{ cm}^3\)
(B) \(1.880 \text{ cm}^3\)
(C) \(1.882 \text{ cm}^3\)
(D) \(1.884 \text{ cm}^3\)
Jawaban: D
Karena \(\dfrac{3}{4}\) bagian gelas sudah terisi air maka perlu mengisi \(1\:-\:\dfrac{3}{4} = \dfrac{1}{4}\) bagian lagi agar gelas terisi penuh dengan air.
Volume air yang ditambahkan = \(\dfrac{1}{4} \times \text{ volume tabung}\)
Volume air yang ditambahkan = \(\dfrac{1}{4} \times \pi \text{r}^2 \text{t}\)
Volume air yang ditambahkan = \(\dfrac{1}{4} \times 3,14\cdot 10^2 \cdot 24\)
Volume air yang ditambahkan = \(\dfrac{1}{\cancel{4}} \times 3,14\cdot 100 \cdot \cancelto{6}{24}\)
Volume air yang ditambahkan = \(314\times 6 = 1.884 \text{ cm}^3\)
Soal 7
Sebuah tabung memiliki volume 37,68 liter. Jika luas alas tabung tersebut adalah 1.256 cm², maka tinggi tabung tersebut adalah … cm
(A) 30 cm
(B) 40 cm
(C) 50 cm
(D) 60 cm
Jawaban: A
Volume tabung = 37,68 liter = 37.680 ml = 37.680 cm³
Volume tabung = luas alas × tinggi
37.680 cm³ = 1.256 cm² × tinggi
Tinggi = 37.680 cm³ ÷ 1.256 cm²
Hitungan:
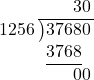
Tinggi = 30 cm
Jadi tinggi tabung tersebut adalah 30 cm
Soal 8
Wilson hendak membuat tabung tertutup dengan ukuran jari-jari 14 cm dan tinggi 22 cm, menggunakan kertas karton. Berapakah luas kertas karton minimal yang dibutuhkan Wilson?
(A) \(3.160 \text{ cm}^2\)
(B) \(3.164 \text{ cm}^2\)
(C) \(3.165 \text{ cm}^2\)
(D) \(3.168 \text{ cm}^2\)
Jawaban: D
Luas karton minimal yang dibutuhkan sama dengan total luas permukaan tabung tertutup
Luas permukaan tabung tertutup = \(2\pi\text{r}(\text{t} + \text{r})\)
Luas permukaan tabung tertutup = \(2\cdot \dfrac{22}{7} \cdot 14(22 +14)\)
Luas permukaan tabung tertutup = \(2\cdot \dfrac{22}{\cancel{7}} \cdot \cancelto{2}{14}(36)\)
Luas permukaan tabung tertutup = \(2\cdot 22 \cdot 2(36)\)
Luas permukaan tabung tertutup = \(2\cdot 22 \cdot 72 = 3.168 \text{ cm}^2\)
Jadi luas karton minimal yang dibutuhkan Wilson adalah \(3.168 \text{ cm}^2\)
Soal 9
Sebuah drum penampungan air berbentuk tabung tanpa tutup, dengan ukuran diameter 56 cm dan tinggi 1,2 meter. Luas permukaan drum tersebut adalah …
(A) \(23.584 \text{ cm}^2\)
(B) \(23.585 \text{ cm}^2\)
(C) \(23.586 \text{ cm}^2\)
(D) \(23.588 \text{ cm}^2\)
Jawaban: A
Jari-jari drum = \(\dfrac{1}{2}\times \text{ diameter}\)
Jari-jari drum = \(\dfrac{1}{2}\times 56 = 28\text{ cm}\)
Tinggi drum = 1,2 meter = 120 cm
Luas permukaan drum tanpa tutup = luas alas + luas selimut
Luas permukaan drum tanpa tutup = \(\pi\text{r}^2 + 2\pi\text{r}\text{t}\)
Luas permukaan drum tanpa tutup = \(\dfrac{22}{7}\cdot 28^2 + 2\cdot \dfrac{22}{7}\cdot 28 \cdot 120\)
Luas permukaan drum tanpa tutup = \(\dfrac{22}{\cancel{7}}\cdot \cancelto{4}{28} \cdot 28 + 2\cdot \dfrac{22}{\cancel{7}}\cdot \cancelto{4}{28} \cdot 120\)
Luas permukaan drum tanpa tutup = \(2464 + 21120\)
Luas permukaan drum tanpa tutup = \(23.584 \text{ cm}^2\)
Soal 10
Sebuah drum berbentuk tabung memiliki kapasitas penyimpanan minyak sebesar 120 liter. Drum tersebut terisi penuh dengan minyak tanah. Jika bagian alas drum mengalami kebocoran dengan debit aliran minyak 2 liter per menit, maka minyak tanah dalam drum tersebut akan habis keluar dalam waktu … jam.
(A) 1 jam
(B) 2 jam
(C) 3 jam
(D) 4 jam
Jawaban: A
Debit aliran minyak yang keluar adalah 2 liter per menit, artinya dalam 1 menit minyak yang keluar dari drum adalah 2 liter.
Karena volume minyak di dalam drum mula-mula adalah 120 liter, maka butuh waktu 120 liter ÷ 2 liter/menit = 60 menit sampai minyak tanah dalam drum tersebut habis.
60 menit = 1 jam
Soal 11
Sebuah tabung memiliki volume 6.336 dm³ dan tinggi 14 dm. Jari-jari tabung tersebut adalah … dm.
(gunakan \(\pi = \frac{22}{7}\)).
(A) 10
(B) 11
(C) 12
(D) 13
Jawaban: C
\(\text{Volume tabung} = \pi \text{r}^2 \text{t}\)
\(6.336 \text{ dm}³ = \frac{22}{7} \cdot \text{r}^2 \cdot 14 \text{ dm}\)
\(6.336 \text{ dm}³ = \frac{22}{\cancel{7}} \cdot \text{r}^2 \cdot \cancelto{2}{14} \text{ dm}\)
\(6.336 = 44 \cdot \text{r}^2\)
\(6.336 \div 44 = \text{r}^2\)
Hitungan:

\(144 = \text{r}^2\)
\(\text{r} = \sqrt{144}\)
\(\text{r} = 12 \text{ dm}\)
Jadi jari-jari tabung tersebut adalah 12 dm
Soal 12
Sebuah tabung memiliki volume 18.840 cm³ dan tinggi 15 cm. Tentukan:
A. Luas alas tabung
B. Jari-jari tabung
(gunakan \(\pi = 3,14\))
A. Menentukan luas alas tabung
Volume tabung = luas alas × tinggi
18.840 cm³ = luas alas × 15 cm
18.840 cm³ ÷ 15 cm = Luas alas
Hitungan:
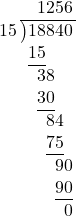
1.256 cm² = luas alas
Jadi luas alas tabung tersebut adalah 1.256 cm²
B. Menentukan jari-jari tabung
Luas alas tabung berbentuk lingkaran, sehingga luas alas tabung sama dengan luas lingkaran
Luas alas = luas lingkaran
Luas alas = \(\pi \text{r}^2\)
1.256 cm² = \(3,14 \cdot \text{r}^2\)
1.256 cm² ÷ 3,14 = \(\text{r}^2\)
125.600 cm²÷ 314 = \(\text{r}^2\)
Hitungan:

\(400 \text{ cm}^2 = \text{r}^2\)
\(\text{r} = \sqrt{400 \text{ cm}^2} = 20 \text{ cm}\)
Jadi jari-jari tabung tersebut adalah 20 cm
