Terdapat tiga buah persegi A, B, dan C yang dihubungkan sehingga ketiga sisinya membentuk segitiga siku-siku.
Luas persegi A adalah \(a^2\).
Luas persegi B adalah \(b^2\).
Luas persegi C adalah \(c^2\).
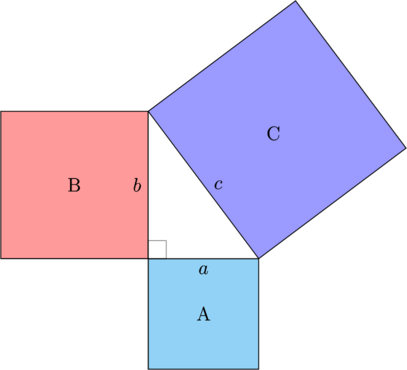
Luas persegi C = luas persegi A + luas persegi B
$$\bbox[yellow, 5px, border: 2px solid red]{c^2 = a^2 + b^2}$$
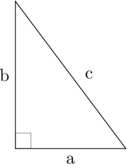
Sisi paling panjang dalam segitiga siku-siku adalah sisi miring (hipotenusa), yaitu sisi \(c\)
Sisi \(a\) dan sisi \(b\) selanjutnya disebut sisi siku-siku.
SOAL LATIHAN
Soal 01
Tentukan nilai \(x\)
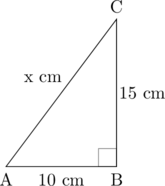
\(\text{AC}^2 = \text{AB}^2 + \text{BC}^2\)
\(x^2 = 10^2 + 15^2\)
\(x^2 = 100 + 225\)
\(x^2 = 325\)
\(x = \sqrt{325}\)
\(x = \sqrt{25 \times 13}\)
\(x = 5 \sqrt{13}\)
Soal 02
Perhatikan gambar berikut

Tentukan panjang AB.
(1) Menghitung panjang EB
Lihat segitiga siku-siku ECB
\(\text{EB}^2 = \text{EC}^2 + \text{BC}^2\)
\(\text{EB}^2 = 7^2 + 24^2\)
\(\text{EB}^2 = 49 + 576\)
\(\text{EB}^2 = 625\)
\(\text{EB}= \sqrt{625} = 25 \text{ cm}\)
(2) Menghitung panjang DB
Lihat segitiga siku-siku EDB
\(\text{EB}^2 = \text{ED}^2 + \text{DB}^2\)
\(25^2 = 15^2 + \text{DB}^2\)
\(625 = 225 + \text{DB}^2\)
\( \text{DB}^2 = 625-225\)
\(\text{DB}= \sqrt{400} = 20 \text{ cm}\)
(3) Menghitung panjang AB
Lihat segitiga siku-siku DAB
\(\text{DB}^2 = \text{DA}^2 + \text{AB}^2\)
\(20^2 = (\sqrt{111})^2 + \text{AB}^2\)
\(400 = 111 + \text{AB}^2\)
\( \text{AB}^2 = 400-111\)
\(\text{AB}= \sqrt{289} = 17 \text{ cm}\)
Jadi, panjang AB adalah 17 cm
Soal 03
Perhatikan gambar berikut
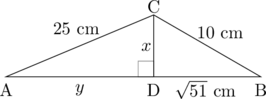
Tentukan nilai \(x + y\)
(1) Menghitung panjang CD
Lihat segitiga siku-siku CDB
\(\text{CB}^2 = \text{CD}^2 + \text{DB}^2\)
\(10^2 = x^2 + (\sqrt{51})^2\)
\(100 = x^2 + 51\)
\( x^2 = 100-51\)
\(x = \sqrt{49} = 7 \text{ cm}\)
(2) Menghitung panjang AD
Lihat segitiga siku-siku ADC
\(\text{AC}^2 = \text{AD}^2 + \text{CD}^2\)
\(25^2 = y^2 + 7^2\)
\(625 = y^2 + 49\)
\( y^2 = 625-49\)
\(y = \sqrt{576} = 24 \text{ cm}\)
Jadi, nilai \(x + y = 7 + 24 = 31 \text{ cm}\)
