A. Pencerminan Terhadap Sumbu x
$$\bbox[yellow, 5pt]{(x, y)\:\xrightarrow{\text{M}_{\text{ sb }x}}\:(x, -y)}$$
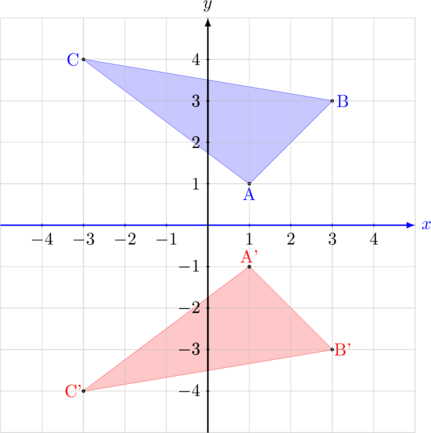
Segitiga ABC dicerminkan terhadap sumbu \(x\)
- \({\text{A}(1, 1)\:\xrightarrow{\text{M}_{\text{ sb }x}}\:\text{A’}(1,-1)}\)
- \({\text{B}(3,3)\:\xrightarrow{\text{M}_{\text{ sb }x}}\:\text{B’}(3,-3)}\)
- \({\text{C}(-3,4)\:\xrightarrow{\text{M}_{\text{ sb }x}}\:\text{C’}(-3,-4)}\)
Bayangan segitiga ABC oleh pencerminan terhadap sumbu \(x\) adalah A’B’C’
B. Pencerminan Terhadap Sumbu y
$$\bbox[yellow, 5pt]{(x, y)\:\xrightarrow{\text{M}_{\text{ sb }y}}\:(-x, y)}$$
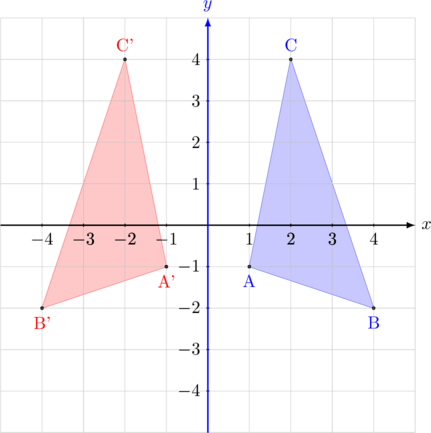
Segitiga ABC dicerminkan terhadap sumbu \(y\)
- \({\text{A}(1, -1)\:\xrightarrow{\text{M}_{\text{ sb }y}}\:\text{A’}(-1,-1)}\)
- \({\text{B}(4,-2)\:\xrightarrow{\text{M}_{\text{ sb }y}}\:\text{B’}(-4,-2)}\)
- \({\text{C}(2,4)\:\xrightarrow{\text{M}_{\text{ sb }y}}\:\text{C’}(-2,4)}\)
Bayangan segitiga ABC oleh pencerminan terhadap sumbu \(y\) adalah A’B’C’
C. Pencerminan Terhadap Garis y = x
$$\bbox[yellow, 5pt]{(x, y)\:\xrightarrow{\text{M}_{ y = x }}\:(y, x)}$$
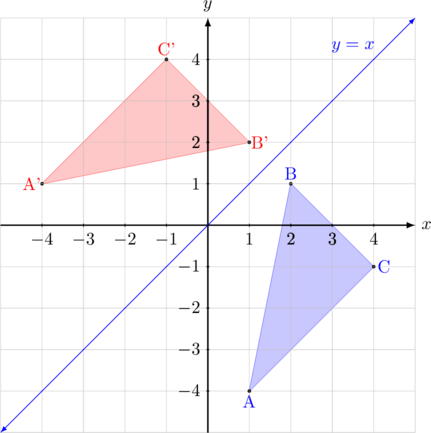
Segitiga ABC dicerminkan terhadap garis \(y = x\)
- \({\text{A}(1,-4)\:\xrightarrow{\text{M}_{ y = x }}\:\text{A’}(-4,1)}\)
- \({\text{B}(2,1)\:\xrightarrow{\text{M}_{ y = x }}\:\text{B’}(1,2)}\)
- \({\text{C}(4,-1)\:\xrightarrow{\text{M}_{ y = x }}\:\text{C’}(-1,4)}\)
Bayangan segitiga ABC oleh pencerminan terhadap garis \(y = x\) adalah A’B’C’
D. Pencerminan Terhadap Garis y = −x
$$\bbox[yellow, 5pt]{(x, y)\:\xrightarrow{\text{M}_{ y = -x }}\:(-y, -x)}$$
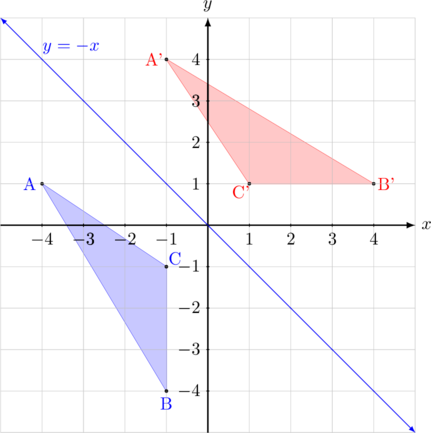
Segitiga ABC dicerminkan terhadap garis \(y = -x\)
- \({\text{A}(-4,1)\:\xrightarrow{\text{M}_{ y = -x }}\:\text{A’}(-1,4)}\)
- \({\text{B}(-1,-4)\:\xrightarrow{\text{M}_{ y = -x }}\:\text{B’}(4,1)}\)
- \({\text{C}(-1,-1)\:\xrightarrow{\text{M}_{ y = -x }}\:\text{C’}(1,1)}\)
Bayangan segitiga ABC oleh pencerminan terhadap garis \(y = -x\) adalah A’B’C’
E. Pencerminan Terhadap Garis x = a
$$\bbox[yellow, 5pt]{(x, y)\:\xrightarrow{\text{M}_{ x = a }}\:(2a-x, y)}$$
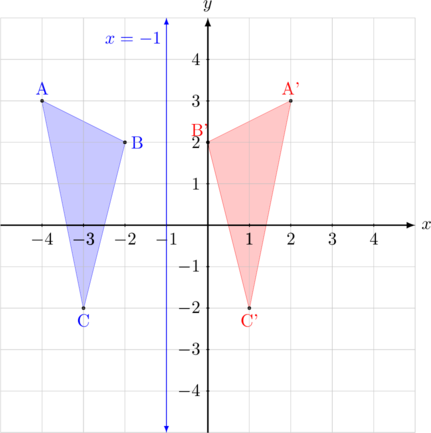
Segitiga ABC dicerminkan terhadap garis \(x = -1\)
- \({\text{A}(-4,3)\:\xrightarrow{\text{M}_{ x = -1 }}\:\text{A’}(2(-1)-(-4),3) = (2, 3)}\)
- \({\text{B}(-2,2)\:\xrightarrow{\text{M}_{ x = -1 }}\:\text{B’}(2(-1)-(-2), 2) = (0, 2)}\)
- \({\text{C}(-3,-2)\:\xrightarrow{\text{M}_{ x =-1 }}\:\text{C’}(2(-1)-(-3), -2) = (1, -2)}\)
Bayangan segitiga ABC oleh pencerminan terhadap garis \(x = -1\) adalah A’B’C’
F. Pencerminan Terhadap Garis y = b
$$\bbox[yellow, 5pt]{(x, y)\:\xrightarrow{\text{M}_{ y = b }}\:(x, 2b-y)}$$
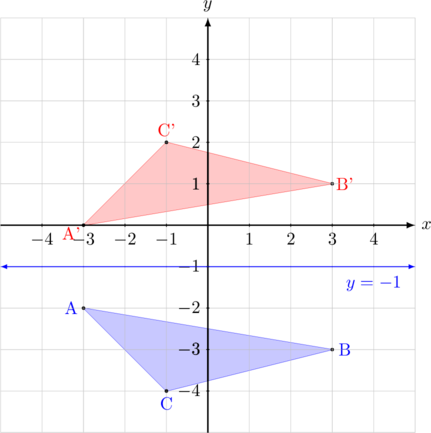
Segitiga ABC dicerminkan terhadap garis \(y = -1\)
- \({\text{A}(-3,-2)\:\xrightarrow{\text{M}_{ y = -1 }}\:\text{A’}(-3, 2(-1)-(-2)) = (-3,0)}\)
- \({\text{B}(3,-3)\:\xrightarrow{\text{M}_{ y = -1 }}\:\text{B’}(3, 2(-1)-(-3)) = (3,1)}\)
- \({\text{C}(-1,-4)\:\xrightarrow{\text{M}_{ y =-1 }}\:\text{C’}(-1,2(-1)-(-4)) = (-1,2)}\)
Bayangan segitiga ABC oleh pencerminan terhadap garis \(y = -1\) adalah A’B’C’
G. Pencerminan Terhadap Titik (a, b)
$$\bbox[yellow, 5pt]{(x, y)\:\xrightarrow{\text{M}_{ (a, b) }}\:(2a-x, 2b-y)}$$
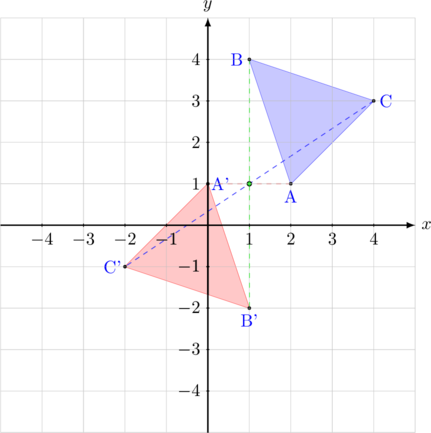
Segitiga ABC dicerminkan terhadap titik \((1, 1)\)
- \({\text{A}(2,1)\:\xrightarrow{\text{M}_{ (1, 1) }}\:\text{A’}(2(1)-2, 2(1)-1) = (0,1)}\)
- \({\text{B}(1,4)\:\xrightarrow{\text{M}_{ (1, 1) }}\:\text{B’}(2(1)-1, 2(1)-4) = (1, -2)}\)
- \({\text{C}(4,3)\:\xrightarrow{\text{M}_{ (1, 1) }}\:\text{C’}(2(1)-4, 2(1)-3) = (-2,-1)}\)
Bayangan segitiga ABC oleh pencerminan terhadap titik \((1, 1)\) adalah A’B’C’
H. Pencerminan Terhadap Titik Asal (0, 0)
$$\bbox[yellow, 5pt]{(x, y)\:\xrightarrow{\text{M}_{ (0, 0) }}\:(-x, -y)}$$
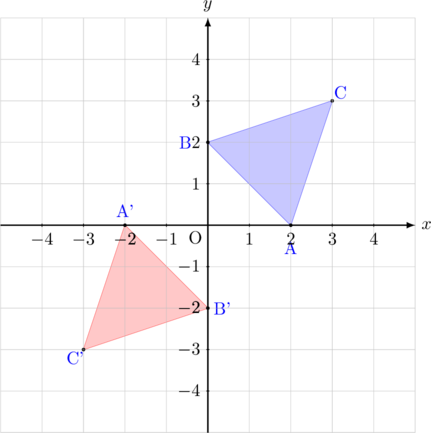
Segitiga ABC dicerminkan terhadap titik asal \((0, 0)\)
- \({\text{A}(2,0)\:\xrightarrow{\text{M}_{ (0, 0) }}\:\text{A’}(-2, 0)}\)
- \({\text{B}(0,2)\:\xrightarrow{\text{M}_{ (0, 0) }}\:\text{B’}(0,-2)}\)
- \({\text{C}(3,3)\:\xrightarrow{\text{M}_{ (0, 0)) }}\:\text{C’}(-3,-3)}\)
Bayangan segitiga ABC oleh pencerminan terhadap titik asal \((0, 0)\) adalah A’B’C’
