Rotasi

A. Rotasi dengan pusat di (0, 0) sebesar 90° searah jarum jam

$$\bbox[yellow, 5pt]{(x, y)\:\xrightarrow{(\text{O}, -90^{\circ})}\:(y, -x)}$$

 

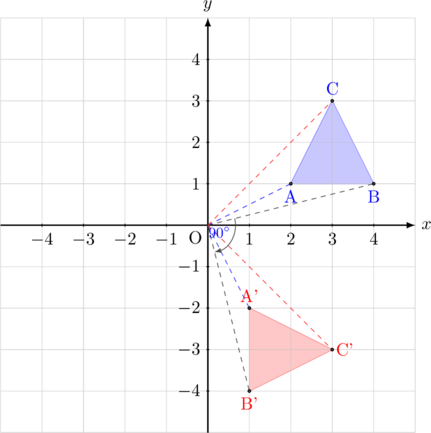
Segitiga ABC dirotasi dengan pusat di \((0, 0)\) sebesar \(90^{\circ}\) searah jarum jam

Bayangan dari segitiga ABC adalah segitiga A’B’C’

B. Rotasi dengan pusat di (0, 0) sebesar 90° berlawanan arah jarum jam

$$\bbox[yellow, 5pt]{(x, y)\:\xrightarrow{(\text{O}, 90^{\circ})}\:(-y, x)}$$

 

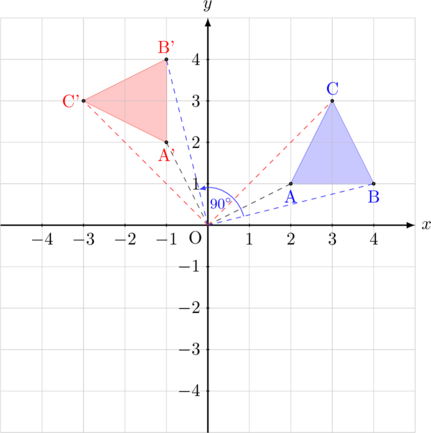
Segitiga ABC dirotasi dengan pusat di \((0, 0)\) sebesar \(90^{\circ}\) berlawanan arah jarum jam

Bayangan dari segitiga ABC adalah segitiga A’B’C’

C. Rotasi dengan pusat di (0, 0) sebesar 180° 

$$\bbox[yellow, 5pt]{(x, y)\:\xrightarrow{(\text{O}, 180^{\circ})}\:(-x, -y)}$$

 

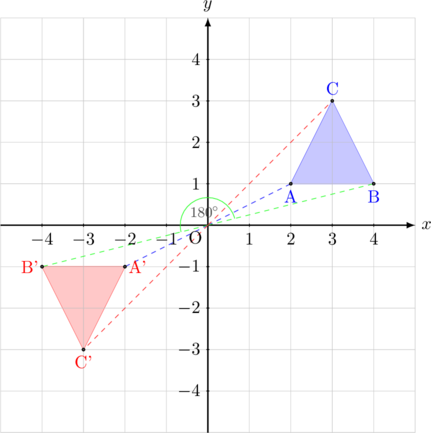
Segitiga ABC dirotasi dengan pusat di \((0, 0)\) sebesar \(180^{\circ}\)

Bayangan dari segitiga ABC adalah segitiga A’B’C’

D. Rotasi dengan pusat di (a, b) sebesar 90° searah jarum jam

$$\bbox[yellow, 5pt]{(x, y)\:\xrightarrow{[(a, b), -90^{\circ}]}\:(y-b+a, -x+a+b)}$$

 

Perhitungan secara matriks:

Bayangan titik \(\text{A}(x, y)\) yang dirotasi dengan pusat \((a, b)\) sebesar \(90^{\circ}\) searah jarum jam adalah \(\text{A’}(x’, y’)\)

\(\begin{bmatrix}x’-a\\y’-b \end{bmatrix}=\begin{bmatrix}\cos \theta & -\sin \theta \\\sin \theta & \cos \theta \end{bmatrix}\begin{bmatrix}x-a \\y-b \end{bmatrix}\)

\(\begin{bmatrix}x’-a\\y’-b \end{bmatrix}=\begin{bmatrix}\cos (-90^{\circ}) & -\sin (-90^{\circ}) \\\sin (-90^{\circ}) & \cos (-90^{\circ}) \end{bmatrix}\begin{bmatrix}x-a \\y-b \end{bmatrix}\)

\(\begin{bmatrix}x’-a\\y’-b \end{bmatrix}=\begin{bmatrix}0 & 1\\-1 & 0 \end{bmatrix}\begin{bmatrix}x-a \\y-b \end{bmatrix}\)

\(\begin{bmatrix}x’-a\\y’-b \end{bmatrix}= \begin{bmatrix}y-b \\-x+a \end{bmatrix}\)

\(x’ – a = y – b\)

\(x’ = y – b + a\)

 

\(y’ – b = -x + a\)

\(y’ = -x + a + b\)

Jadi bayangan titik \(\text{A}(x, y)\)  adalah \(\text{A}'(y – b + a, -x + a + b)\)

E. Rotasi dengan pusat di (a, b) sebesar 90° berlawanan arah jarum jam

$$\bbox[yellow, 5pt]{(x, y)\:\xrightarrow{[(a, b), 90^{\circ}]}\:(-y + b + a, x – a + b)}$$

 

Perhitungan secara matriks:

Bayangan titik \(\text{A}(x, y)\) yang dirotasi dengan pusat \((a, b)\) sebesar \(90^{\circ}\) berlawanan arah jarum jam adalah \(\text{A’}(x’, y’)\)

\(\begin{bmatrix}x’-a\\y’-b \end{bmatrix}=\begin{bmatrix}\cos \theta & -\sin \theta \\\sin \theta & \cos \theta \end{bmatrix}\begin{bmatrix}x-a \\y-b \end{bmatrix}\)

\(\begin{bmatrix}x’-a\\y’-b \end{bmatrix}=\begin{bmatrix}\cos (90^{\circ}) & -\sin (90^{\circ}) \\\sin (90^{\circ}) & \cos (90^{\circ}) \end{bmatrix}\begin{bmatrix}x-a \\y-b \end{bmatrix}\)

\(\begin{bmatrix}x’-a\\y’-b \end{bmatrix}=\begin{bmatrix}0 & -1\\1 & 0 \end{bmatrix}\begin{bmatrix}x-a \\y-b \end{bmatrix}\)

\(\begin{bmatrix}x’-a\\y’-b \end{bmatrix}= \begin{bmatrix}-y +b\\x- a \end{bmatrix}\)

\(x’ – a = -y + b\)

\(x’ = -y + b + a\)

 

\(y’ – b = x – a\)

\(y’ = x – a + b\)

Jadi bayangan titik \(\text{A}(x, y)\)  adalah \(\text{A}'(-y + b + a, x – a + b)\)

F. Rotasi dengan pusat di (a, b) sebesar 180°

$$\bbox[yellow, 5pt]{(x, y)\:\xrightarrow{[(a, b), 180^{\circ}]}\:(-x + 2a, -y + 2b)}$$

 

Perhitungan secara matriks:

Bayangan titik \(\text{A}(x, y)\) yang dirotasi dengan pusat \((a, b)\) sebesar \(180^{\circ}\) adalah \(\text{A’}(x’, y’)\)

\(\begin{bmatrix}x’-a\\y’-b \end{bmatrix}=\begin{bmatrix}\cos \theta & -\sin \theta \\\sin \theta & \cos \theta \end{bmatrix}\begin{bmatrix}x-a \\y-b \end{bmatrix}\)

\(\begin{bmatrix}x’-a\\y’-b \end{bmatrix}=\begin{bmatrix}\cos (180^{\circ}) & -\sin (180^{\circ}) \\\sin (180^{\circ}) & \cos (180^{\circ}) \end{bmatrix}\begin{bmatrix}x-a \\y-b \end{bmatrix}\)

\(\begin{bmatrix}x’-a\\y’-b \end{bmatrix}=\begin{bmatrix}-1 & 0\\0 & -1 \end{bmatrix}\begin{bmatrix}x-a \\y-b \end{bmatrix}\)

\(\begin{bmatrix}x’-a\\y’-b \end{bmatrix}= \begin{bmatrix}-x+a\\-y+b\end{bmatrix}\)

\(x’ – a = -x + a\)

\(x’ = -x + 2a\)

\(y’ – b = -y + b\)

\(y’ = -y + 2b\)

Jadi bayangan titik \(\text{A}(x, y)\)  adalah \(\text{A}'(-x + 2a, -y + 2b)\)