Soal 01
Sebuah kawat dengan panjang 500 cm akan dibuat kerangka balok dengan panjang 25 cm. Jika volume baloknya maksimum, tentukan ukuran lebar dan tinggi balok tersebut.

Misal ukuran lebar balok = \(x\) dan ukuran tinggi balok = \(y\)
Keliling balok = 4 × (panjang + lebar + tinggi)
\(500 = 4\times (25 + x + y)\)
\(500 = 100 + 4x + 4y\)
\(400 = 4x + 4y\)
Bagi kedua ruas dengan 4,
\(100 = x + y\)
\(y = 100\:-\:x\dotso \color{red} (1)\)
Volume balok = panjang × lebar × tinggi
\(V = 25xy\dotso \color{red} (2)\)
Substitusikan persamaan (1) ke persamaan (2)
\(V = 25x(100\:-\:x)\)
\(V = 2500x\:-\:25x^2\)
Volume balok akan maksimum jika \(V’ = 0\)
\(2500\:-\:50x = 0\)
\(50x = 2500\)
\(x = 50\)
\(y = 100\:-\:50 = 50\)
Jadi ukuran lebar balok adalah 50 cm dan tingginya juga 50 cm
Soal 02
Tentukan luas maksimum persegi panjang yang dapat dibuat pada daerah yang dibatasi kurva \(y = -x^2 + 8\) dan sumbu X.
Kurva \(y = -x^2 + 8\) berbentuk parabola yang membuka ke bawah.
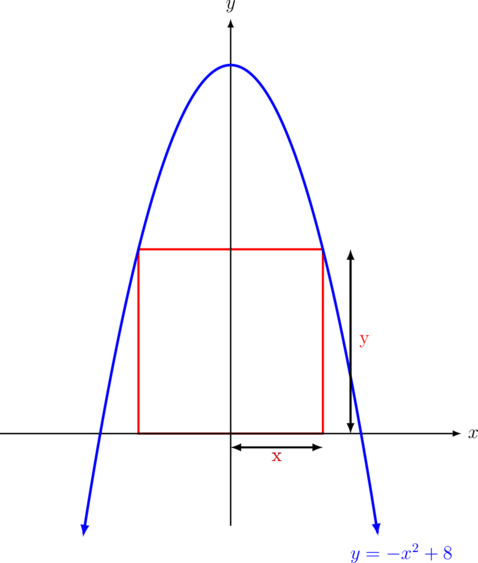
Luas persegi panjang = \(2x \cdot y\)
\(\text{L} = 2x(-x^2 + 8)\)
\(\text{L} = -2x^3 + 16x\)
Luas persegi panjang maksimum jika \(\text{L}’ = 0\)
\(\text{L}’ = -6x^2 + 16 = 0\)
\(-6x^2 = -16\)
\(x^2 = \dfrac{8}{3}\)
\(x = \sqrt{\dfrac{8}{3}} = \dfrac{2\sqrt{2}}{\sqrt{3}} = \dfrac{2}{3}\sqrt{6}\)
\(\text{L}_{\text{max}} = -2\left( \dfrac{2}{3}\sqrt{6} \right)^3 + 16\left( \dfrac{2}{3}\sqrt{6}\right)\)
\(\text{L}_{\text{max}} = -2\left( \dfrac{16\sqrt{6}}{9}\right) + \left( \dfrac{32}{3}\sqrt{6}\right)\)
\(\text{L}_{\text{max}} = \left(- \dfrac{32}{9}\sqrt{6}\right) + \left( \dfrac{96}{9}\sqrt{6}\right)\)
\(\text{L}_{\text{max}} = \dfrac{64}{9}\sqrt{6} \)
Jadi luas maksimum persegi panjang tersebut adalah \(\dfrac{64}{9}\sqrt{6} \)
Soal 03
Sebuah peluru ditembakkan vertikal ke atas. Jika tinggi \(h\) meter setelah \(t\) detik dirumuskan dengan \(h(t) = -t^3 + \dfrac{5}{2}t^2 + 2t + 12\), maka tentukan tinggi maksimum yang dapat dicapai peluru tersebut.
Tinggi maksium dapat dicapai peluru jika \(h'(t) = 0\)
\(h'(t) = -3t^2 + 5t + 2 = 0\)
\(3t^2\:-\:5t\:-\:2 = 0\)
\((3t + 1)(t \:-\: 2) = 0\)
\(3t + 1 = 0 \rightarrow t = -\dfrac{1}{3}\:\:\color{red} \text{ TM}\)
\(t\:-\:2 = 0 \rightarrow t = 2\text{ s}\)
\(h(2) = -(2)^3 + \dfrac{5}{2}(2)^2 + 2(2) + 12\)
\(h(2) = -8 + 10 + 4 + 12\)
\(h(2) = 18 \text{ meter}\)
Jadi ketinggian maksimum yang dapat dicapai peluru tersebut adalah 18 meter.
Soal 04
Sebuah industri rumah tangga memproduksi \(x\) buah roti dengan biaya totalnya \((6x^2 \:-\:400x + 20.000)\) rupiah. Jika setiap roti dijual dengan harga \(4000\:-\:5x\) rupiah, maka tentukan keuntungan maksimum yang diperoleh.
Keuntungan = penjualan x buah roti − biaya total
\(\text{K} = x(4000\:-\:5x) \:-\: (6x^2 \:-\:400x + 20.000)\)
\(\text{K} = 4000x\:-\:5x^2\:-\:6x^2 + 400x\:-\:20.000\)
\(\text{K} = -11x^2 + 4.400x\:-\:20.000\)
Agar keuntungannya maksimum maka \(\text{K}’ = 0\)
\(-22x + 4.400 = 0\)
\(x = \dfrac{4.400}{22} = 200\)
Keuntungan maksimumnya:
\(\text{K}_{\text{max}}= -11(200)^2 + 4.400(200)\:-\:20.000\)
\(\text{K}_{\text{max}}= -440.000 + 880.000\:-\:20.000\)
\(\text{K}_{\text{max}}= \text{ Rp420.000,00}\)
Soal 05
Kawat sepanjang 120 m akan dibuat kerangka seperti gambar di bawah ini.

Tentukan luas maksimum daerah yang dibentuk oleh kawat tersebut.
Kawat sepanjang 120 m akan dibuat dibentuk menjadi bangun dengan kawat mendatar sejumlah \(3p\) dan kawat vertikal sejumlah \(4l\)
\(3p + 4l = 120\)
\(3p = 120 \:-\:4l\)
\(p = 40\:-\:\dfrac{4}{3}l\dotso \color{red} (1)\)
Luas bangun yang terbentuk \(L = p \cdot 2l\dotso \color{red} (2)\)
Substitusikan persamaan (1) ke persamaan (2)
\(L = (40\:-\:\dfrac{4}{3}l) \cdot 2l\)
\(L = 80l\:-\:\dfrac{8}{3}l^2\)
Agar luas maksimum maka \(L’ = 0\)
\(80\:-\:\dfrac{16}{3}l = 0\)
\(80 = \dfrac{16}{3}l\)
\(l = \dfrac{3}{\cancel{16}} \times \cancelto{5}{80}\)
\(l = 15 \text{ meter}\)
Substitusikan nilai \(l\) ini ke persamaan \(L\) untuk mendapatkan luas maksimum
\(L_{\text{max}} = 80(15)\:-\:\dfrac{8}{3}(15)^2\)
\(L_{\text{max}} = 1200\:-\:600\)
\(L_{\text{max}} = 600 \text{ m}^2\)
Soal 06
Sebuah setengah lingkaran berjari-jari 10 cm, di dalamnya terdapat sebuah persegi panjang. Tentukan luas maksimum persegi panjang yang dapat dibuat.

Persamaan lingkaran berpusat di (0, 0) dan berjari-jari 10 adalah \(x^2 + y^2 = 10^2\) atau dapat ditulis \(y = \sqrt{100 \:-\:x^2}\)
Persegi panjang yang berada di dalam setengah lingkaran memiliki ukuran panjang \(2x\) dan lebar \(y\) sehingga persamaan luasnya adalah:
\(L = 2x \cdot y\)
Substitusikan \(y = \sqrt{100 \:-\:x^2}\) ke dalam persamaan \(L\)
\(L = 2x \cdot \sqrt{100 \:-\:x^2}\)
Agar luas maksimum maka \(L’ = 0\)
Misal:
\(u = 2x \rightarrow u’ = 2\)
\(v = \sqrt{100 \:-\:x^2}\)
\( v’ = (-2x) \cdot \dfrac{1}{2} (100 \:-\: x^2)^{-\frac{1}{2}}\)
\(v’ = -\dfrac{x}{\sqrt{100 \:-\: x^2}}\)
\(L’ = u’\cdot v + u \cdot v’\)
\(0 = 2 \cdot \sqrt{100 \:-\:x^2} + 2x \cdot -\dfrac{x}{\sqrt{100 \:-\: x^2}}\)
\(0 = \dfrac{2(100 \:-\:x^2) \:-\: 2x^2}{\sqrt{100 \:-\: x^2}}\)
\(0 = \dfrac{200\:-\:4x^2}{\sqrt{100 \:-\: x^2}}\)
\(200\:-\:4x^2 = 0\)
\(4x^2 = 200\)
\(x^2 = 50\)
\(x = \sqrt{50} = 5\sqrt{2}\)
\(L_{\text{max}} = 2( 5\sqrt{2}) \cdot \sqrt{100 \:-\:( 5\sqrt{2})^2}\)
\(L_{\text{max}} = 10 \sqrt{2}\cdot \sqrt{100 \:-\:50}\)
\(L_{\text{max}} = 10 \sqrt{2}\cdot 5\sqrt{2}\)
\(L_{\text{max}} = 100\)
