Soal 01
Dua gabus terapung di permukaan air laut dan berjarak 1 meter satu sama lain. Keduanya berada di puncak gelombang dan diantara kedua gabus terdapat sebuah lembah gelombang. Jika frekuensi gelombang adalah 10 Hz, panjang gelombang dan cepat rambat gelombang berturut-turut adalah…
(A) 0,5 m dan 5 m/s
(B) 0,5 m dan 10 m/s
(C) 1 m dan 10 m/s
(D) 1,5 m dan 10 m/s
(E) 5 m dan 10 m/s
Jawaban: C
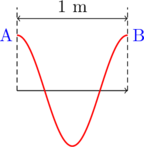
\(1 \lambda = 1 \text{ meter}\)
\(\color{blue}v = \lambda \cdot f\)
\(v = 1 \cdot 10\)
\(v = 10 \text{ m/s}\)
Soal 02
Gelombang transversal merambat dari A ke B dengan cepat rambat 12 m/s pada frekuensi 4 Hz dan amplitudo 5 cm. Jika jarak AB = 18 meter, maka banyaknya gelombang yang terjadi sepanjang AB adalah…
(A) 4
(B) 6
(C) 7
(D) 8
(E) 9
Jawaban: B
Menentukan panjang gelombang
\(\color{blue}v = \lambda \cdot f\)
\(12 = \lambda \cdot 4\)
\(\lambda = \dfrac{12}{4} = 3 \text{ meter}\)
1 gelombang panjangnya 3 meter
Karena jarak AB = 18 meter maka banyaknya gelombang adalah 18 ÷ 3 = 6 gelombang
Soal 03
Persamaan gelombang berjalan dinyatakan dengan persamaan \(y = 0,1 \sin \pi(5x\:-\:8t)\); \(x\) dan \(y\) dalam meter dan \(t\) dalam detik.
(1) frekuensi gelombang 5 Hz
(2) panjang gelombang 40 cm
(3) cepat rambat gelombang 20 m/s
(4) kecepatan maksimum partikel \(0,8 \pi\) m/s
Pernyataan yang benar adalah…
(A) (1) dan (3)
(B) (1) dan (4)
(C) (2) dan (4)
(D) (1), (2), dan (3)
(E) (1), (2), (3), dan (4)
Jawaban: C
\(y = 0,1 \sin \pi(5x\:-\:8t)\)
\(y = 0,1 \sin (5\pi x\:-\:8\pi t)\)
\(\omega = 8\pi\)
\(2\pi \cdot f= 8\pi\)
\(f= 4 \text{ Hz}\)
\(k = \dfrac{2\pi}{\lambda}\)
\(5\pi = \dfrac{2\pi}{\lambda}\)
\(\lambda = \dfrac{2}{5} \text{ m} = 40 \text{ cm}\)
\(v = \lambda \cdot f\)
\(v = \dfrac{2}{5} \cdot 4 = 1,6 \text{ m/s}\)
\(v_{\text{max}} = \omega \cdot \text{ A}\)
\(v_{\text{max}} = 8 \pi \cdot 0,1 = 0,8 \pi \text{ m/s}\)
Soal 04
Gelombang stasioner memiliki persamaan \(y = 10 \cos 2\pi x \cdot \sin 20\pi t\) dengan \(x\) dan \(y\) dalam satuan meter dan \(t\) dalam sekon. Cepat rambat gelombang tersebut adalah…
(A) 10 m/s
(B) 12 m/s
(C) 14 m/s
(D) 16 m/s
(E) 20 m/s
Jawaban: A
Menentukan frekuensi gelombang dari informasi kecepatan sudut
Kecepatan sudut diperoleh dari koefisien \(t\)
\(\omega = 20 \pi \text{ rad/s}\)
\(2\pi \cdot f = 20 \pi\)
\(f = 10 \text{ Hz}\)
Menentukan panjang gelombang dari informasi bilangan gelombang
Bilangan gelombang diperoleh dari koefisien \(x\)
\(k = 2\pi\)
\(\dfrac{2\pi}{\lambda} = 2\pi\)
\(\lambda = 1\text{ meter}\)
Menentukan cepat rambat gelombang
\(v = \lambda \times f\)
\(v = 1 \times 10\)
\(v = 10 \text{ m/s}\)
Soal 05
Simpangan gelombang stasioner dinyatakan dengan persamaan \(y = 10 \cos 0,5 \pi x \cdot \sin 40 \pi t \) \(x\) dan \(y\) dalam cm dan \(t\) dalam sekon, maka:
(1) Amplitudo gelombang stasioner pada suatu titik yang berjarak \(\dfrac{2}{3}\) m dari ujung pantulnya adalah 5 cm
(2) Letak simpul ketiga berjarak 5 m dari ujung pantul
(3) Letak perut kelima berjarak 8 m dari ujung pantul
(4) Cepat rambat gelombang stasioner tersebut 8 m/s
Pernyataan yang benar adalah…
(A) 1, 2, 3, dan 4
(B) 1, 2, dan 3
(C) 1 dan 3
(D) 2 dan 4
(E) 4 saja
Jawaban: B
\(y = 10 \cos 0,5 \pi x \cdot \sin 40 \pi t \)
\(\omega = 40 \pi\)
\(2\pi f = 40 \pi\)
\(f = 20 \text{ Hz}\)
\(k = 0,5 \pi\)
\(\dfrac{2\pi}{\lambda} = \dfrac{1}{2} \pi\)
\(\lambda = 4 \text{ cm}\)
Karena \(x\) dinyatakan dalam cm maka \(\lambda\) memiliki satuan cm juga
(1) Menentukan amplitudo gelombang stasioner
\(\text{A}_{s} = 10 \cos 0,5 \pi x\)
\(\text{A}_{s} = 10 \cos \left(\dfrac{1}{2} \pi \cdot \dfrac{2}{3}\right)\)
\(\text{A}_{s} = 10 \cos 60^{\circ}\)
\(\text{A}_{s} = 10 \cdot \dfrac{1}{2} = 5 \text{ cm}\)
Karena \(y\) dalam satuan cm maka amplitudo juga bersatuan cm
(2) Menentukan letak simpul ketiga dari ujung pantul
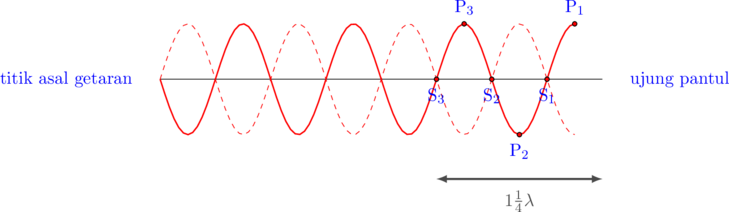
Jarak simpul ketiga = \(1\dfrac{1}{4}\lambda = \dfrac{5}{4}\cdot 4 = 5 \text{ cm}\)
(3) Menentukan letak perut kelima dari ujung pantul
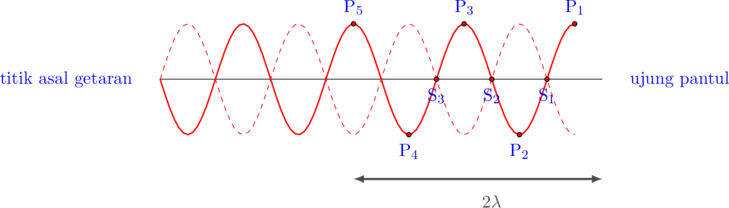
Jarak perut kelima= \(2\lambda = 2\cdot 4 = 8\text{ cm}\)
(4) Menentukan cepat rambat gelombang
\(v = \lambda \cdot f\)
\(v = 4 \text{ cm } \cdot 20 \text{ Hz} = 80 \text{ cm/s}\)
\(v = 0,8 \text{ m/s}\)
