Soal 1
Pak Joko mempunyai 3 petak sawah, masing-masing seluas \(\dfrac{1}{4}\) hektare. Sawah tersebut telah ditanami jagung seluas \(\dfrac{5}{8}\) hektare. Luas sawah Pak Joko yang belum ditanami jagung adalah … hektare
(A) \(\dfrac{1}{8}\)
(B) \(\dfrac{1}{7}\)
(C) \(\dfrac{1}{6}\)
(D) \(\dfrac{1}{5}\)
Jawaban: A
Luas seluruh sawah milik Pak Joko adalah \(3 \times \dfrac{1}{4} = \dfrac{3}{4}\) hektare
\(\dfrac{5}{8}\) hektare sawah sudah ditanami jagung, maka luas sawah Pak Joko yang belum ditanami jagung adalah \(\dfrac{3}{4}\:-\:\dfrac{5}{8} = \dfrac{1}{8}\) hektare.
Soal 2
Filan memiliki uang sejumlah Rp850.000,00. Ia menggunakan 50% uang tersebut untuk membeli kalkulator dan \(\dfrac{1}{5}\) bagian lagi untuk membeli pizza. Sisa uang yang ada kemudian ia tabung. Uang yang ditabung sejumlah …
(A) Rp235.000,00
(B) Rp250.000,00
(C) Rp255.000,00
(D) Rp265.000,00
Jawaban: C
Langkah 1
Menghitung uang yang digunakan untuk membeli kalkulator
\(50 \% \times 850.000\)
\(\dfrac{50}{100} \times 850.000\)
\(\dfrac{1}{2} \times 850.000\)
\(425.000\)
Uang yang digunakan Filan untuk membeli kalkulator sebesar Rp425.000,00
Langkah 2
Menghitung uang yang digunakan untuk membeli pizza
\(\dfrac{1}{5}\times 850.000\)
\(\dfrac{850.000}{5}\)
\(170.000\)
Uang yang digunakan Filan untuk membeli pizza sebesar Rp170.000,00
Langkah 3
Menghitung uang yang ditabung Filan
Uang yang ditabung = Rp850.000,00 − total uang yang sudah dibelanjakan
Uang yang ditabung = Rp850.000 − Rp425.000 − Rp170.000
Uang yang ditabung = Rp255.000,00
Soal 3
Joni berangkat dari Bantul pukul 09.30 WIB menuju Purworejo mengendarai sepeda motor dengan kecepatan rata-rata 50 km/jam. Jarak dari Bantul ke Purworejo adalah 40 km. Pada pukul berapa Joni sampai di Purworejo?
(A) 10.08 WIB
(B) 10.10 WIB
(C) 10.12 WIB
(D) 10.18 WIB
Jawaban: D
Menghitung waktu yang diperlukan oleh Joni untuk sampai di Purworejo
\(\color{blue} \text{Jarak} = \text{kecepatan} \times \text{ waktu}\)
\(40 \text{ km} = 50 \text{ km/jam} \times \text{ t}\)
\(\text{ t} = 40 \text{ km} ÷ 50 \text{ km/jam}\)
\(\text{ t} = \dfrac{40}{50} \text{ jam}\)
\(\text{ t} = \dfrac{4}{5} \text{ jam}\)
\(\text{ t} = \dfrac{4}{5} \times 60 \text{ menit}\)
\(\text{ t} = \dfrac{4}{\cancel{5}} \times \cancelto{12}{60} \text{ menit}\)
\(\text{ t} = 48\text{ menit}\)
Waktu sampai = 09.30 + 48 menit
pukul 09.00 lebih 78 menit (ingat bahwa 60 menit = 1 jam)
pukul 09.00 lebih 1 jam 18 menit
Jadi, Joni sampai di Purworejo pukul 10.18 WIB
Soal 4
Jarak antara Yogyakarta dengan Kebumen adalah 115 km. Ciko bersepeda motor dari Yogyakarta menuju Kebumen dengan kecepatan rata-rata 60 km/jam. Pada rute yang sama, Dodi bersepeda motor dari Kebumen dengan kecepatan rata-rata 40 km/jam. Jika mereka berangkat dalam waktu yang sama pukul 08.15 WIB, mereka akan berpapasan pada pukul …
(A) 09.20 WIB
(B) 09.24 WIB
(C) 09.34 WIB
(D) 09.44 WIB
Jawaban: B
Misal:
- Jarak yang ditempuh Ciko dari Yogyakarta sampai berpapasan dengan Dodi adalah \(\text{s}_1\)
- Kecepatan rata-rata sepeda motor Ciko adalah \(\text{v}_1\)
- Jarak yang ditempuh Dodi dari Kebumen sampai berpapasan dengan Ciko adalah \(\text{s}_2\)
- Kecepatan rata-rata sepeda motor Dodi adalah \(\text{v}_2\)
Karena jarak antara Yogyakarta dengan Kebumen 115 km, maka \(\text{s}_1 + \text{s}_2 = 112 \text{ km}\)
Ingat rumus jarak
\(\color{blue} \text{s} = \text{v} \times \text{ t}\)
\(\text{s}_1 + \text{s}_2 = 115 \text{ km}\)
\(\text{v}_1 \cdot \text{ t} + \text{v}_2 \cdot \text{ t} = 115 \text{ km}\)
\(60 \text{ km/jam} \cdot \text{ t} + 40 \text{ km/jam}\cdot \text{ t} = 115 \text{ km}\)
\(60\text{ t} + 40\text{ t} = 115 \)
\(100\text{ t} = 115 \)
\(\text{t} = 115 \div 100\)
\(\text{t} = \dfrac{115}{100} \text{ jam}\)
\(\text{t} = \dfrac{23}{20} \text{ jam}\)
\(\text{t} = \dfrac{23}{\cancel{20}} \times \cancelto{3}{60} \text{ menit}\)
\(\text{t} = 69\text{ menit}\)
\(\text{t} = 1 \text{ jam }9\text{ menit}\)
Waktu mereka berpapasan adalah 08.15 + 1 jam 9 menit = pukul 09.24 WIB
Soal 5
Jarak rumah Mahesa sampai ke sekolah adalah 4 km. Mahesa berangkat ke sekolah menggunakan sepeda dengan kecepatan rata-rata 10 km/jam. Bel masuk sekolah berbunyi pada pukul 07.00 WIB. Mahesa tiba di sekolah 20 menit sebelum bel masuk sekolah berbunyi. Pada pukul berapa Mahesa berangkat ke sekolah?
(A) 06.16 WIB
(B) 06.17 WIB
(C) 06.18 WIB
(D) 06.19 WIB
Jawaban: A
Langkah 1: Menghitung waktu perjalanan Mahesa untuk sampai ke sekolah
\(\color{blue} \text{Jarak} = \text{kecepatan} \times \text{ waktu}\)
\(4 \text{ km} = 10 \text{ km/jam} \times \text{ t}\)
\(\text{t} = 4 \text{ km} \div 10 \text{ km/jam}\)
\(\text{t} = \dfrac{4}{10} \text{ jam}\)
\(\text{t} = \dfrac{4}{\cancel{10}} \times \cancelto{6}{60} \text{ menit}\)
\(\text{t} = 24 \text{ menit}\)
Langkah 2: Menentukan waktu Mahesa tiba di sekolah
Mahesa tiba di sekolah 20 menit sebelum pukul 07.00 yaitu pukul 06.40 WIB
Langkah 2: Menentukan waktu Mahesa berangkat ke sekolah
pukul 06.40 − 24 menit = 06.16
Jadi, Mahesa berangkat ke sekolah pada pukul 06.16 WIB
Soal 6
Pekarangan rumah Pak Ronald berbentuk persegi panjang dengan panjang 30 meter dan lebar 18 meter. Pak Ronald akan menggambar pekarangannya pada denah dengan skala 1 : 500. Luas pekarangan Pak Ronald pada denah adalah … cm².
(A) 18,6
(B) 20,8
(C) 21,6
(D) 22,4
Jawaban: C
Skala denah 1 : 500, artinya setiap jarak 1 cm pada denah mewakili ukuran sebenarnya 500 cm.
Panjang pekarangan sesungguhnya 30 meter = 3.000 cm
Panjang pekarangan pada denah = 3.000 ÷ 500 = 6 cm
Lebar pekarangan sesungguhnya 18 meter = 1.800 cm
Lebar pekarangan pada denah = 1.800 ÷ 500 = 3,6 cm
Luas pekarangan pada denah = 6 cm × 3,6 cm = 21,6 cm²
Soal 7
Dari sebuah kran Pak Budi mengisi bak penampungan air yang berbentuk balok dengan ukuran panjang dan lebar sisi bagian dalam bak tersebut 12 dm dan 6 dm, kedalaman bak tersebut 10 dm. Bak tersebut dapat terisi penuh dengan air dalam waktu \(\dfrac{1}{3}\) jam. Debit aliran kran adalah … liter/menit.
(A) 28
(B) 30
(C) 32
(D) 36
Jawaban: D
Volume bak = panjang × lebar × tinggi
Volume bak = 12 dm × 6 dm × 10 dm
Volume bak = 720 dm³ = 720 liter
Waktu pengisian = \(\dfrac{1}{3}\) jam
Waktu pengisian = \(\dfrac{1}{3}\times 60\) menit
Waktu pengisian = 20 menit
Debit = volume ÷ waktu
Debit aliran kran = 720 liter ÷ 20 menit
Debit aliran kran = 36 liter/menit
Soal 8
Jarak Sleman dan Gombong adalah 100 km. Pada pukul 08.30 WIB, Ani mengendarai mobil dari Sleman menuju Gombong dengan kecepatan rata-rata 60 km/jam. Setengah jam kemudian, Budi bersepeda motor dari Gombong ke Sleman melalui rute yang sama dengan kecepatan rata-rata 40 km/jam. Ani dan Budi akan berpapasan pada pukul …
(A) 09.34 WIB
(B) 09.42 WIB
(C) 10.12 WIB
(D) 10.15 WIB
Jawaban: B
Misal:
- Jarak yang ditempuh Ani dari Sleman sampai berpapasan dengan Budi adalah \(\text{s}_1\)
- Kecepatan rata-rata mobil Ani adalah \(\text{v}_1\)
- Waktu perjalanan Ani sampai berpapasan dengan Budi adalah \(\text{t} + \frac{1}{2}\) (karena Ani duluan berangkat \(\color{red} \frac{1}{2}\) jam)
- Jarak yang ditempuh Budi dari Gombong sampai berpapasan dengan Ani adalah \(\text{s}_2\)
- Kecepatan rata-rata sepeda motor Budi adalah \(\text{v}_2\)
- Waktu perjalanan Budi sampai berpapasan dengan Ani adalah \(\text{t}\)
Karena jarak antara Sleman dengan Gombong 100 km, maka \(\text{s}_1 + \text{s}_2 = 100\text{ km}\)
Ingat rumus jarak
\(\color{blue} \text{s} = \text{v} \times \text{ t}\)
\(\text{s}_1 + \text{s}_2 = 100 \text{ km}\)
\(\text{v}_1 \cdot (\text{t} + \frac{1}{2}) + \text{v}_2 \cdot \text{t} = 100 \text{ km}\)
\(60 \text{ km/jam}\cdot (\text{t} + \frac{1}{2}) + 40\text{ km/jam} \cdot \text{t} = 100 \text{ km}\)
\(60 (\text{t} + \frac{1}{2}) + 40\text{t} = 100\)
\(60\text{t} + 30 + 40\text{t} = 100\)
\(60\text{t} + 40\text{t} =100\:-\:30\)
\(100\text{t} = 70\)
\(\text{t} = \dfrac{70}{100} \text{ jam}\)
\(\text{t} = \dfrac{7}{10} \text{ jam}\)
Waktu perjalanan Ani sampai berpapasan dengan Budi adalah \(\text{t} + \frac{1}{2}\)
\(= \dfrac{7}{10} + \dfrac{1}{2} \text{ jam}\)
\(= \dfrac{6}{5} \text{ jam}\)
\(= 1 \text{ jam} + \dfrac{1}{5}\times 60\text{ menit}\)
\(= 1 \text{ jam} + 12\text{ menit}\)
Pukul 08.30 + 1 jam 12 menit = 09.42
Jadi, mereka akan berpapasan pada pukul 09.42 WIB
Soal 9
Berikut ini adalah data penjualan tas ransel di Toko Star.
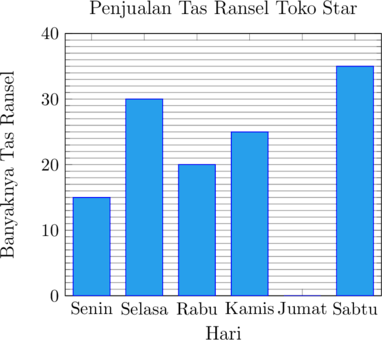
Jika total penjualan tas ransel di Toko Star selama 6 hari adalah 153 tas, jumlah tas ransel yang terjual pada hari Jumat adalah…
(A) 24
(B) 26
(C) 28
(D) 30
Jawaban: C
Tas yang terjual pada hari Senin = 15
Tas yang terjual pada hari Selasa = 30
Tas yang terjual pada hari Rabu = 20
Tas yang terjual pada hari Kamis = 25
Tas yang terjual pada hari Jumat = x
Tas yang terjual pada hari Sabtu = 35
15 + 30 + 20 + 25 + x + 35 = 153
125 + x = 153
x = 153 − 125
x = 28
Jadi, banyaknya tas ransel yang terjual pada hari Jumat sebanyak 28 tas.
Soal 10
Berikut ini adalah data tinggi badan 45 murid kelas 5 SD Kencana.
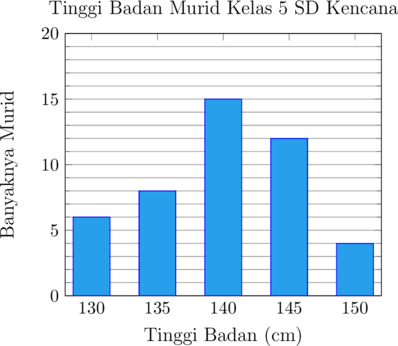
Jumlah murid dengan tinggi badan lebih dari 140 cm adalah…
(A) 12 anak
(B) 14 anak
(C) 16 anak
(D) 31 anak
Jawaban: C
Jumlah murid dengan tinggi badan 145 cm = 12 anak
Jumlah murid dengan tinggi badan 150 cm = 4 anak
Jadi, jumlah murid dengan tinggi badan lebih dari 140 cm adalah 12 + 4 = 16 anak
