Quiz-summary
0 of 17 questions completed
Pertanyaan:
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
Information
Dear Students,
Welcome to today’s quiz! This is your opportunity to demonstrate what you’ve learned so far, so do your best. Please keep in mind that you have a maximum of 45 minutes to complete all the questions. Make sure to manage your time wisely and answer each question thoughtfully.
Good luck!
Anda telah menyelesaikan kuis sebelumnya. Oleh karena itu, Anda tidak dapat memulainya lagi.
Quiz is loading...
You must sign in or sign up to start the quiz.
You have to finish following quiz, to start this quiz:
Hasil
0 dari 17 pertanyaan terjawab dengan benar
Waktu Anda:
Time has elapsed
Anda telah meraih 0 dari 0 poin, (0)
Categories
- Not categorized 0%
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- Dijawab
- Ragu-Ragu
-
Pertanyaan 1 dari 17
1. Pertanyaan
1 pointsAnton, Andi dan Andre suka berenang. Anton berenang di kolam renang umum setiap 5 hari sekali. Andi berenang di kolam renang umum setiap 4 hari sekali, dan Andre berenang di kolam renang umum setiap 3 hari sekali. Jika pada tanggal 04 Desember 2022 mereka berenang di kolam renang umum yang sama, pada tanggal berapa mereka akan berenang bersama lagi?
Benar
Soal cerita tersebut dapat diselesaikan dengan menghitung nilai KPK dari 5, 4, dan 3
KPK dari 5, 4, dan 3 adalah \(5 \times 4 \times 3 = 60\)
Mereka akan berenang kembali 60 hari setelah tanggal 04 Desember 2022, yaitu tanggal 02 Februari 2023
Salah
Soal cerita tersebut dapat diselesaikan dengan menghitung nilai KPK dari 5, 4, dan 3
KPK dari 5, 4, dan 3 adalah \(5 \times 4 \times 3 = 60\)
Mereka akan berenang kembali 60 hari setelah tanggal 04 Desember 2022, yaitu tanggal 02 Februari 2023
-
Pertanyaan 2 dari 17
2. Pertanyaan
1 pointsHasil dari \(\dfrac{2\:-\:1\frac{2}{3}}{1\:-\:\dfrac{1}{\frac{1}{1\:-\:\frac{2}{3}}}}\) adalah …
Benar
\(\dfrac{2\:-\:1\frac{2}{3}}{1\:-\:\dfrac{1}{\frac{1}{1\:-\:\frac{2}{3}}}}\)
\(\dfrac{2\:-\:\frac{5}{3}}{1\:-\:\dfrac{1}{\frac{1}{3}}}\)
\(\dfrac{\frac{1}{3}}{1\:-\:3}\)
\(\dfrac{\frac{1}{3}}{-2}\)
\(-\dfrac{1}{6}\)
Salah
\(\dfrac{2\:-\:1\frac{2}{3}}{1\:-\:\dfrac{1}{\frac{1}{1\:-\:\frac{2}{3}}}}\)
\(\dfrac{2\:-\:\frac{5}{3}}{1\:-\:\dfrac{1}{\frac{1}{3}}}\)
\(\dfrac{\frac{1}{3}}{1\:-\:3}\)
\(\dfrac{\frac{1}{3}}{-2}\)
\(-\dfrac{1}{6}\)
-
Pertanyaan 3 dari 17
3. Pertanyaan
1 pointsOperasi hitung “@” mengikuti urutan aturan sebagai berikut:
Langkah 1: kuadratkan bilangan pertama
Langkah 2: kurangkan hasil langkah (1) dari hasil perkalian antara bilangan pertama dengan bilangan kedua
Langkah 3: jumlahkan hasil langkah (2) dengan pangkat tiga bilangan kedua
Hasil dari (3 @ −1) @ 2 adalah …
Benar
Misalkan bilangan pertama adalah A dan bilangan kedua adalah B
A @ B = \((\text{A} \times \text{B})\:-\:\text{A}^2 + \text{B}^3\)
3 @ −1 = \([3 \times (-1)]\:-\:3^2 + (-1)^3\)
3 @ −1 = \(-3\:-\:9\:-\:1\)
3 @ −1 = \(-13\)
(3 @ −1) @ 2 = −13 @ 2
−13 @ 2 = \((-13 \times 2)\:-\:(-13)^2 + 2^3\)
−13 @ 2 = \(-187\)
Salah
Misalkan bilangan pertama adalah A dan bilangan kedua adalah B
A @ B = \((\text{A} \times \text{B})\:-\:\text{A}^2 + \text{B}^3\)
3 @ −1 = \([3 \times (-1)]\:-\:3^2 + (-1)^3\)
3 @ −1 = \(-3\:-\:9\:-\:1\)
3 @ −1 = \(-13\)
(3 @ −1) @ 2 = −13 @ 2
−13 @ 2 = \((-13 \times 2)\:-\:(-13)^2 + 2^3\)
−13 @ 2 = \(-187\)
-
Pertanyaan 4 dari 17
4. Pertanyaan
1 pointsSeorang ayah hendak membagikan tanah warisan kepada 3 orang anaknya. Anak pertama mendapatkan \(\frac{1}{5}\) bagian tanah warisan, anak kedua mendapatkan \(\frac{1}{2}\) bagian dari tanah yang anak pertama dapatkan, dan anak ketiga mendapatkan \(\frac{1}{3}\) dari sisa tanah warisan ayah. Jika setelah pembagian tanah warisan, masih ada 3,5 hektar tanah, maka luas tanah keseluruhan yang dimiliki ayah mula-mula adalah …
Benar
Anak Pertama
Anak pertama memperoleh \(\frac{1}{5}\) bagian tanah warisan
Anak Kedua
Anak pertama memperoleh \(\frac{1}{2}\times\frac{1}{5} = \frac{1}{10}\) bagian tanah warisan
Anak Ketiga
Sisa tanah = \(1\:-\:\frac{1}{5} \:-\:\frac{1}{10} = \frac{7}{10}\)
Anak pertama memperoleh \(\frac{1}{3}\times \frac{7}{10} = \frac{7}{30}\) bagian tanah warisan
Sisa Tanah Akhir
\(3,5 \text{ Ha} = 1\:-\:\frac{1}{5}\:-\:\frac{1}{10}\:-\:\frac{7}{30}\) bagian
\(3,5 \text{ Ha} = \frac{7}{15}\) bagian
Luas Tanah Ayah Semula
\(3,5 \text{ Ha} = \frac{7}{15}\) bagian
\(1 \text{ bagian} = \frac{15}{7}\times 3,5 \text{ Ha}\)
\(1 \text{ bagian} = 7,5\text{ Ha}\)
Salah
Anak Pertama
Anak pertama memperoleh \(\frac{1}{5}\) bagian tanah warisan
Anak Kedua
Anak pertama memperoleh \(\frac{1}{2}\times\frac{1}{5} = \frac{1}{10}\) bagian tanah warisan
Anak Ketiga
Sisa tanah = \(1\:-\:\frac{1}{5} \:-\:\frac{1}{10} = \frac{7}{10}\)
Anak pertama memperoleh \(\frac{1}{3}\times \frac{7}{10} = \frac{7}{30}\) bagian tanah warisan
Sisa Tanah Akhir
\(3,5 \text{ Ha} = 1\:-\:\frac{1}{5}\:-\:\frac{1}{10}\:-\:\frac{7}{30}\) bagian
\(3,5 \text{ Ha} = \frac{7}{15}\) bagian
Luas Tanah Ayah Semula
\(3,5 \text{ Ha} = \frac{7}{15}\) bagian
\(1 \text{ bagian} = \frac{15}{7}\times 3,5 \text{ Ha}\)
\(1 \text{ bagian} = 7,5\text{ Ha}\)
-
Pertanyaan 5 dari 17
5. Pertanyaan
1 pointsDiketahui:
\(\text{Semesta himpunan} = \lbrace x|\: 20 < x < 40, \: x\in \text{ bilangan asli} \rbrace\)
\(\text{A} = \lbrace x|\: 20 < x < 40, \: x\in \text{ bilangan ganjil } \rbrace\)
\(\text{B} = \lbrace x|\: 20 < x < 40, \: x\in \text{ bilangan komposit} \rbrace\)
\(\text{C} = \lbrace x|\: 20 < x < 40, \: x\in \text{ kelipatan 7} \rbrace\)
\(\text{A}^{\text{c}} \cap \text{ B } \cap \text{ C } = \dotso\)
Benar
\(\text{Semesta himpunan} = \lbrace 21, 22, 23, \dotso, 39 \rbrace\)
\(\text{A} = \lbrace 21, 23, 25, 27, 29, 31, 33, 35, 37, 39 \rbrace\)
Komplemen dari A adalah bilangan-bilangan yang bukan anggota dari himpunan A tetapi ada di semesta
\(\text{A}^{\text{c}} = \lbrace 22, 24, 26, \color{red} 28 \color{black}, 30, 32, 34, 36, 38 \rbrace\)
Bilangan komposit adalah bilangan yang bukan prima karena memiliki faktor lebih dari 2
\(\text{B} = \lbrace 21, 24, 25, 26, 27, \color{red} 28 \color{black}, 30, 32, 33, 34, 35, 36, 38, 39 \rbrace\)
\(\text{C} = \lbrace 21, \color{red} 28 \color{black}, 35\rbrace\)
\(\cap = \text{ irisan}\)
Untuk menentukan irisan, carilah bilangan yang merupakan anggota dari \(\text{A}^{\text{c}}\), \(\text{B}\), dan juga \(\text{C}\), bilangan tersebut adalah 28
\(\text{Jadi, }\text{A}^{\text{c}} \cap \text{ B } \cap \text{ C } = \lbrace 28 \rbrace\)
Salah
\(\text{Semesta himpunan} = \lbrace 21, 22, 23, \dotso, 39 \rbrace\)
\(\text{A} = \lbrace 21, 23, 25, 27, 29, 31, 33, 35, 37, 39 \rbrace\)
Komplemen dari A adalah bilangan-bilangan yang bukan anggota dari himpunan A tetapi ada di semesta
\(\text{A}^{\text{c}} = \lbrace 22, 24, 26, \color{red} 28 \color{black}, 30, 32, 34, 36, 38 \rbrace\)
Bilangan komposit adalah bilangan yang bukan prima karena memiliki faktor lebih dari 2
\(\text{B} = \lbrace 21, 24, 25, 26, 27, \color{red} 28 \color{black}, 30, 32, 33, 34, 35, 36, 38, 39 \rbrace\)
\(\text{C} = \lbrace 21, \color{red} 28 \color{black}, 35\rbrace\)
\(\cap = \text{ irisan}\)
Untuk menentukan irisan, carilah bilangan yang merupakan anggota dari \(\text{A}^{\text{c}}\), \(\text{B}\), dan juga \(\text{C}\), bilangan tersebut adalah 28
\(\text{Jadi, }\text{A}^{\text{c}} \cap \text{ B } \cap \text{ C } = \lbrace 28 \rbrace\)
-
Pertanyaan 6 dari 17
6. Pertanyaan
1 pointsPerhatikan pernyataan di bawah ini:
(i) \(16x^2\:-\:25 = (4x\:-\:5)(4x\:-\:5)\)
(ii) \(9x^2 + x = x(9x)\)
(iii) \(3x^2\:-\:7 = (\sqrt{3} x + \sqrt{7})(\sqrt{3} x \:-\:\sqrt{7})\)
(iv) \(21x^2\:-\:134x + 85 = (7x\:-\:5)(3x\:-\:17)\)
Pernyataan yang benar adalah …
Benar
Gunakan rumus pemfaktoran \(x^2 \:-\:y^2 = ( x + y)(x\:-\:y)\)
(i) \((4x)^2\:-\:5^2 = (4x + 5)(4x\:-\:5)\)
(ii) \(9x^2 + x = x(9x + 1)\)
(iii) \((\sqrt{3} x)^2\:-\:(\sqrt{7})^2 = (\sqrt{3} x + \sqrt{7})(\sqrt{3} x \:-\:\sqrt{7})\)
(iv) \(21x^2\:-\:134x + 85 = (7x\:-\:5)(3x\:-\:17)\)
Pernyataan yang benar adalah (iii) dan (iv)
Salah
Gunakan rumus pemfaktoran \(x^2 \:-\:y^2 = ( x + y)(x\:-\:y)\)
(i) \((4x)^2\:-\:5^2 = (4x + 5)(4x\:-\:5)\)
(ii) \(9x^2 + x = x(9x + 1)\)
(iii) \((\sqrt{3} x)^2\:-\:(\sqrt{7})^2 = (\sqrt{3} x + \sqrt{7})(\sqrt{3} x \:-\:\sqrt{7})\)
(iv) \(21x^2\:-\:134x + 85 = (7x\:-\:5)(3x\:-\:17)\)
Pernyataan yang benar adalah (iii) dan (iv)
-
Pertanyaan 7 dari 17
7. Pertanyaan
1 pointsPersamaan garis yang melalui titik \((-1, -11)\) dan \((2, 7)\) adalah …
Benar
Misal:
\((x_1, y_1) = (-1, -11) \text{ dan } (x_2, y_2) = (2, 7)\)
Rumus persamaan garis yang melalui dua titik adalah:
\(\color{blue}\dfrac{y\:-\:y_1}{y_2\:-\:y_1} = \dfrac{x\:-\:x_1}{x_2\:-\:x_1}\)
\(\dfrac{y\:-\:(-11)}{7\:-\:(-11)} = \dfrac{x\:-\:(-1)}{2\:-\:(-1)}\)
\(\dfrac{y + 11}{7 + 11} = \dfrac{x + 1}{2 + 1}\)
\(\dfrac{y + 11}{18} = \dfrac{x + 1}{3}\)
Selanjutnya, kalikan silang
\(3(y + 11) = 18(x + 1)\)
\(3y + 33 = 18x + 18\)
Bagi kedua ruas dengan 3,
\(y + 11 = 6x + 6\)
\(y = 6x + 6\:-\:11\)
\(y = 6x \:-\:5\)
Salah
Misal:
\((x_1, y_1) = (-1, -11) \text{ dan } (x_2, y_2) = (2, 7)\)
Rumus persamaan garis yang melalui dua titik adalah:
\(\color{blue}\dfrac{y\:-\:y_1}{y_2\:-\:y_1} = \dfrac{x\:-\:x_1}{x_2\:-\:x_1}\)
\(\dfrac{y\:-\:(-11)}{7\:-\:(-11)} = \dfrac{x\:-\:(-1)}{2\:-\:(-1)}\)
\(\dfrac{y + 11}{7 + 11} = \dfrac{x + 1}{2 + 1}\)
\(\dfrac{y + 11}{18} = \dfrac{x + 1}{3}\)
Selanjutnya, kalikan silang
\(3(y + 11) = 18(x + 1)\)
\(3y + 33 = 18x + 18\)
Bagi kedua ruas dengan 3,
\(y + 11 = 6x + 6\)
\(y = 6x + 6\:-\:11\)
\(y = 6x \:-\:5\)
-
Pertanyaan 8 dari 17
8. Pertanyaan
1 pointsPersamaan garis yang tegak lurus dengan garis \(2x + 3y = 12\) dan melalui titik \((0, -3)\) adalah …
Benar
Langkah 1: menentukan gradien garis \(2x + 3y = 12\)
\(3y = -2x + 12\)
\(y = -\frac{2}{3}x + 4\)
Gradien garis \(2x + 3y = 12\) adalah \(\text{m}_1 = -\frac{2}{3}\)
Langkah 2: syarat dua garis saling tegak lurus \(\text{m}_1 \times \text{m}_2 = -1\)
\(\text{m}_1\times \text{m}_2 = -1\)
\(-\frac{2}{3} \times \text{m}_2 = -1\)
\(\text{m}_2 = -1 \times (-\frac{3}{2})\)
\(\text{m}_2 = \frac{3}{2}\)
Langkah 3: Menentukan persamaan garis
Persamaan garis melalui titik \((x_1, y_1) = (0, -3)\) dan bergradien \(\text{m}_2 = \frac{3}{2}\) adalah:
\(y \:-\:y_1 = \text{m}_2 (x\:-\:x_1)\)
\(y \:-\:(-3) = \frac{3}{2} (x\:-\:0)\)
\(y + 3 = \frac{3}{2}x\)
Kalikan kedua ruas dengan 2
\(2y + 6 = 3x\)
\(2y \:-\:3x = -6\)
Salah
Langkah 1: menentukan gradien garis \(2x + 3y = 12\)
\(3y = -2x + 12\)
\(y = -\frac{2}{3}x + 4\)
Gradien garis \(2x + 3y = 12\) adalah \(\text{m}_1 = -\frac{2}{3}\)
Langkah 2: syarat dua garis saling tegak lurus \(\text{m}_1 \times \text{m}_2 = -1\)
\(\text{m}_1\times \text{m}_2 = -1\)
\(-\frac{2}{3} \times \text{m}_2 = -1\)
\(\text{m}_2 = -1 \times (-\frac{3}{2})\)
\(\text{m}_2 = \frac{3}{2}\)
Langkah 3: Menentukan persamaan garis
Persamaan garis melalui titik \((x_1, y_1) = (0, -3)\) dan bergradien \(\text{m}_2 = \frac{3}{2}\) adalah:
\(y \:-\:y_1 = \text{m}_2 (x\:-\:x_1)\)
\(y \:-\:(-3) = \frac{3}{2} (x\:-\:0)\)
\(y + 3 = \frac{3}{2}x\)
Kalikan kedua ruas dengan 2
\(2y + 6 = 3x\)
\(2y \:-\:3x = -6\)
-
Pertanyaan 9 dari 17
9. Pertanyaan
1 pointsDiketahui fungsi \(g(x) = b\:-\:ax\). Jika \(g(3) = -13\) dan \(g(-5) = 27\), maka nilai \(g(-1) = \dotso\)
Benar
\(g(x) = b\:-\:ax\)
\(g(3) = b\:-\:3a = -13\dotso\dotso \color{red} (1)\)
\(g(-5) = b + 5a = 27\dotso\dotso \color{red} (2)\)
Kurangkan persamaan (1) dengan persamaan (2) untuk eliminasi \(b\)
\(-8a = -40\)
\(a = 5\)
Selanjutnya substitusikan \(a = 5\) ke persamaan (1)
\(b\:-\:3(5) = -13\)
\(b \:-\:15 = -13\)
\(b = -13 + 15\)
\(b = 2\)
Persamaan fungsi \(g\) adalah \(g(x) = 2\:-\:5x\)
\(g(-1) = 2\:-\:5(-1)\)
\(g(-1) = 2 + 5 = 7\)
Salah
\(g(x) = b\:-\:ax\)
\(g(3) = b\:-\:3a = -13\dotso\dotso \color{red} (1)\)
\(g(-5) = b + 5a = 27\dotso\dotso \color{red} (2)\)
Kurangkan persamaan (1) dengan persamaan (2) untuk eliminasi \(b\)
\(-8a = -40\)
\(a = 5\)
Selanjutnya substitusikan \(a = 5\) ke persamaan (1)
\(b\:-\:3(5) = -13\)
\(b \:-\:15 = -13\)
\(b = -13 + 15\)
\(b = 2\)
Persamaan fungsi \(g\) adalah \(g(x) = 2\:-\:5x\)
\(g(-1) = 2\:-\:5(-1)\)
\(g(-1) = 2 + 5 = 7\)
-
Pertanyaan 10 dari 17
10. Pertanyaan
1 pointsSebuah belah ketupat ABCD memiliki panjang diagonal AC = 14 cm. Jika keliling belah ketupat tersebut adalah 100 cm, maka luas belah ketupat adalah …
Benar
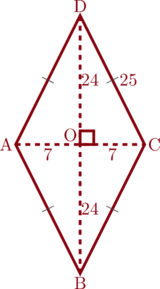
Langkah 1: menghitung panjang DO
Perhatikan segitiga siku-siku DOC
Panjang DC adalah keliling belah ketupat dibagi 4, sehingga DC = \(\frac{100}{4} = 25\text{ cm}\)
Panjang DO dapat dihitung menggunakan rumus pythagoras
\(\text{DC}^2 = \text{DO}^2 + \text{OC}^2\)
\(25^2 = \text{DO}^2 + 7^2\)
\(625 = \text{DO}^2 + 49\)
\(\text{DO}^2 = 625\:-\:49\)
\(\text{DO}^2 =576\)
\(\text{DO} = \sqrt{576} = 24\text{ cm}\)
Langkah 2: menghitung luas belah ketupat
\(\text{Luas ABCD} = \dfrac{\text{d}_1 \times \text{d}_2}{2}\)
\(\text{Luas ABCD} = \dfrac{\text{AC} \times \text{BD}}{2}\)
\(\text{Luas ABCD} = \dfrac{14 \times 48}{2}\)
\(\text{Luas ABCD} = \dfrac{14 \times \cancelto{24}{48}}{\cancel{2}}\)
\(\text{Luas ABCD} = 336 \text{ cm}^2\)
Salah

Langkah 1: menghitung panjang DO
Perhatikan segitiga siku-siku DOC
Panjang DC adalah keliling belah ketupat dibagi 4, sehingga DC = \(\frac{100}{4} = 25\text{ cm}\)
Panjang DO dapat dihitung menggunakan rumus pythagoras
\(\text{DC}^2 = \text{DO}^2 + \text{OC}^2\)
\(25^2 = \text{DO}^2 + 7^2\)
\(625 = \text{DO}^2 + 49\)
\(\text{DO}^2 = 625\:-\:49\)
\(\text{DO}^2 =576\)
\(\text{DO} = \sqrt{576} = 24\text{ cm}\)
Langkah 2: menghitung luas belah ketupat
\(\text{Luas ABCD} = \dfrac{\text{d}_1 \times \text{d}_2}{2}\)
\(\text{Luas ABCD} = \dfrac{\text{AC} \times \text{BD}}{2}\)
\(\text{Luas ABCD} = \dfrac{14 \times 48}{2}\)
\(\text{Luas ABCD} = \dfrac{14 \times \cancelto{24}{48}}{\cancel{2}}\)
\(\text{Luas ABCD} = 336 \text{ cm}^2\)
-
Pertanyaan 11 dari 17
11. Pertanyaan
1 pointsVolume bola terbesar yang dapat dimasukkan ke dalam sebuah kubus dengan panjang rusuk 42 cm adalah …
Benar
Volume bola terbesar adalah volume bola yang memiliki diameter 42 cm
Jari-jari bola = \(\frac{1}{2} \times 42 = 21 \text{ cm}\)
\(\text{V} = \frac{4}{3}\cdot \pi \cdot \text{ r}^3\)
\(\text{V} = \frac{4}{\cancel{3}}\cdot \frac {22}{\cancel{7}}\cdot \cancelto{3}{21} \cdot \cancelto {7}{21} \cdot 21\)
\(\text{V} = 38.808 \text{ cm}^3\)
Salah
Volume bola terbesar adalah volume bola yang memiliki diameter 42 cm
Jari-jari bola = \(\frac{1}{2} \times 42 = 21 \text{ cm}\)
\(\text{V} = \frac{4}{3}\cdot \pi \cdot \text{ r}^3\)
\(\text{V} = \frac{4}{\cancel{3}}\cdot \frac {22}{\cancel{7}}\cdot \cancelto{3}{21} \cdot \cancelto {7}{21} \cdot 21\)
\(\text{V} = 38.808 \text{ cm}^3\)
-
Pertanyaan 12 dari 17
12. Pertanyaan
1 pointsDua buah dadu dilambungkan 1 kali. Peluang muncul jumlah kedua mata dadu merupakan bilangan prima adalah …
Benar
Jumlah kedua mata dadu merupakan bilangan prima:
(1, 1), (1, 2), (1, 4), (1, 6), (2, 1), (2, 3), (2, 5), (3, 2), (3, 4), (4, 1), (4, 3), (5, 2), (5, 6), (6, 1), dan (6, 5)
\(\text{n(A)} = 15\)
\(\text{P(A)} = \frac{\text{n(A)} }{\text{n(S)} }\)
\(\text{P(A)} = \frac{15}{36}\)
\(\text{P(A)} = \frac{5}{12}\)
Salah
Jumlah kedua mata dadu merupakan bilangan prima:
(1, 1), (1, 2), (1, 4), (1, 6), (2, 1), (2, 3), (2, 5), (3, 2), (3, 4), (4, 1), (4, 3), (5, 2), (5, 6), (6, 1), dan (6, 5)
\(\text{n(A)} = 15\)
\(\text{P(A)} = \frac{\text{n(A)} }{\text{n(S)} }\)
\(\text{P(A)} = \frac{15}{36}\)
\(\text{P(A)} = \frac{5}{12}\)
-
Pertanyaan 13 dari 17
13. Pertanyaan
1 pointsLook at the figure below:
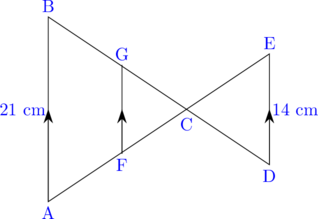
If AF : FE = 1 : 3, then FG = …
Benar
\(\dfrac{\text{AB}}{\text{DE}} = \dfrac{\text{AC}}{\text{CE}}\)
\(\dfrac{21 \text{ cm}}{14 \text{ cm}} = \dfrac{\text{AC}}{\text{CE}}\)
\(\dfrac{3}{2} = \dfrac{\text{AC}}{\text{CE}}\)
\(\dfrac{3}{2} = \dfrac{\text{AF + FC}}{\text{CE}}\)
\(3\text{CE} = 2 \text{AF} + 2\text{FC}\dotso\dotso \color{red} (1)\)
\(\dfrac{\text{AF}}{\text{FE}} = \dfrac{1}{3}\)
\(\dfrac{\text{AF}}{\text{FC + CE}} = \dfrac{1}{3}\)
\(3\text{AF} = \text{FC} + \text{CE}\)
\(\text{CE} = 3\text{AF}\:-\:\text{FC}\dotso\dotso \color{red} (2)\)
Eliminasi persamaan (1) dan (2)
\(3\text{CE} = 2 \text{AF} + 2\text{FC}\dotso\dotso \color{red} (1) | \times 3\)
\(\text{CE} = 3\text{AF}\:-\:\text{FC}\dotso\dotso \color{red} (2) | \times 2\)
Kurangkan persamaan (1) dengan persamaan (2)
\(9\text{CE} = 6 \text{AF} + 6\text{FC}\)
\(2\text{CE} = 6\text{AF}\:-\:2\text{FC}\)
\(7 \text{CE} = 8 \text{FC}\)
\( \text{CE} = \frac{8}{7} \text{FC}\)
\(\dfrac{\text{FG}}{\text{DE}} = \dfrac{\text{FC}}{\text{CE}}\)
\(\dfrac{\text{FG}}{14} = \dfrac{\cancel{\text{FC}}}{ \frac{8}{7}\cancel{\text{FC}}}\)
\(\dfrac{\text{FG}}{14} = \dfrac{7}{8}\)
\(8\text{FG} = 14 \times 7\)
\(\text{FG} = \frac{98}{8}\)
\(\text{FG} = 12,25 \text{ cm}\)
Salah
\(\dfrac{\text{AB}}{\text{DE}} = \dfrac{\text{AC}}{\text{CE}}\)
\(\dfrac{21 \text{ cm}}{14 \text{ cm}} = \dfrac{\text{AC}}{\text{CE}}\)
\(\dfrac{3}{2} = \dfrac{\text{AC}}{\text{CE}}\)
\(\dfrac{3}{2} = \dfrac{\text{AF + FC}}{\text{CE}}\)
\(3\text{CE} = 2 \text{AF} + 2\text{FC}\dotso\dotso \color{red} (1)\)
\(\dfrac{\text{AF}}{\text{FE}} = \dfrac{1}{3}\)
\(\dfrac{\text{AF}}{\text{FC + CE}} = \dfrac{1}{3}\)
\(3\text{AF} = \text{FC} + \text{CE}\)
\(\text{CE} = 3\text{AF}\:-\:\text{FC}\dotso\dotso \color{red} (2)\)
Eliminasi persamaan (1) dan (2)
\(3\text{CE} = 2 \text{AF} + 2\text{FC}\dotso\dotso \color{red} (1) | \times 3\)
\(\text{CE} = 3\text{AF}\:-\:\text{FC}\dotso\dotso \color{red} (2) | \times 2\)
Kurangkan persamaan (1) dengan persamaan (2)
\(9\text{CE} = 6 \text{AF} + 6\text{FC}\)
\(2\text{CE} = 6\text{AF}\:-\:2\text{FC}\)
\(7 \text{CE} = 8 \text{FC}\)
\( \text{CE} = \frac{8}{7} \text{FC}\)
\(\dfrac{\text{FG}}{\text{DE}} = \dfrac{\text{FC}}{\text{CE}}\)
\(\dfrac{\text{FG}}{14} = \dfrac{\cancel{\text{FC}}}{ \frac{8}{7}\cancel{\text{FC}}}\)
\(\dfrac{\text{FG}}{14} = \dfrac{7}{8}\)
\(8\text{FG} = 14 \times 7\)
\(\text{FG} = \frac{98}{8}\)
\(\text{FG} = 12,25 \text{ cm}\)
-
Pertanyaan 14 dari 17
14. Pertanyaan
1 pointsJika \((\sqrt{3} + \sqrt{5} + 1)(\sqrt{3} + \sqrt{5} \:-\: 1) = a + b\sqrt{15}\:\), maka nilai \(2a + b = \dotso\)
Benar
Gunakan rumus \(\color{blue} (x + y)(x\:-\:y) = x^2 \:-\:y^2\)
\(\color{blue} x = \sqrt{3} + \sqrt{5}\)
\(\color{blue} y = 1\)
\((\sqrt{3} + \sqrt{5} + 1)(\sqrt{3} + \sqrt{5} \:-\: 1)\)
\((\sqrt{3} + \sqrt{5})^2 \:-\:1^2\)
\((\sqrt{3})^2 + 2\sqrt{3}\cdot \sqrt{5} + (\sqrt{5})^2 \:-\:1\)
\(3 + 2\sqrt{15} + 5 \:-\:1\)
\(7 + 2\sqrt{15} = a + b\sqrt{15}\)
\(a = 7 \text{ dan } b = 2\)
\(\text{ Jadi, } 2a + b = 2(7) + 2 = 16\)
Salah
Gunakan rumus \(\color{blue} (x + y)(x\:-\:y) = x^2 \:-\:y^2\)
\(\color{blue} x = \sqrt{3} + \sqrt{5}\)
\(\color{blue} y = 1\)
\((\sqrt{3} + \sqrt{5} + 1)(\sqrt{3} + \sqrt{5} \:-\: 1)\)
\((\sqrt{3} + \sqrt{5})^2 \:-\:1^2\)
\((\sqrt{3})^2 + 2\sqrt{3}\cdot \sqrt{5} + (\sqrt{5})^2 \:-\:1\)
\(3 + 2\sqrt{15} + 5 \:-\:1\)
\(7 + 2\sqrt{15} = a + b\sqrt{15}\)
\(a = 7 \text{ dan } b = 2\)
\(\text{ Jadi, } 2a + b = 2(7) + 2 = 16\)
-
Pertanyaan 15 dari 17
15. Pertanyaan
1 pointsDi kelas 9A terdapat 40 siswa, rata-rata nilai ulangan statistika siswa laki-laki adalah 85 dan rata-rata nilai ulangan statistika siswa perempuan adalah 90. Jika jumlah siswa laki-laki 4 kurangnya dari jumlah siswa perempuan, maka rata-rata nilai ulangan statistika di kelas 9A adalah …
Benar
Misal:
\(\text{n}_1 = \text{banyaknya siswa laki-laki}\)
\(\bar {x}_1 = \text{rata-rata nilai statistika siswa laki-laki}\)
\(\text{n}_2 = \text{banyaknya siswa perempuan}\)
\(\bar {x}_2 = \text{rata-rata nilai statistika siswa perempuan}\)
\(\bar {x}_{\text{ gabungan}} = \text{rata-rata nilai statistika kelas 9A}\)
Gunakan rumus rata-rata gabungan:
\(\color{blue} \bar {x}_{\text{ gabungan}} = \dfrac{\bar {x}_1 \cdot \text{n}_1 + \bar {x}_2 \cdot \text{n}_2 }{\text{n}_1 + \text{n}_2}\)
Jumlah siswa laki-laki 4 kurangnya dari jumlah siswa perempuan, artinya \(\text{n}_1 = \text{n}_2\:-\:4\)
Jumlah seluruh siswa di kelas 9A adalah 40 siswa,
\(\text{n}_1 + \text{n}_2 = 40\)
\(\text{n}_2\:-\:4 + \text{n}_2 = 40\)
\(2\text{n}_2 = 40 + 4\)
\(\text{n}_2 = \frac{44}{2} = 22\)
\(\text{n}_1 = 18\)
Banyaknya siswa perempuan ada 22 orang dan siswa laki-laki ada 18 orang
\(\bar {x}_{\text{ gabungan}} = \dfrac{85\cdot 18 + 90 \cdot 22}{18 + 22}\)
\(\bar {x}_{\text{ gabungan}} = \dfrac{1530 + 1980}{40}\)
\(\bar {x}_{\text{ gabungan}} = \dfrac{3510}{40}\)
\(\bar {x}_{\text{ gabungan}} = 87,75\)
Salah
Misal:
\(\text{n}_1 = \text{banyaknya siswa laki-laki}\)
\(\bar {x}_1 = \text{rata-rata nilai statistika siswa laki-laki}\)
\(\text{n}_2 = \text{banyaknya siswa perempuan}\)
\(\bar {x}_2 = \text{rata-rata nilai statistika siswa perempuan}\)
\(\bar {x}_{\text{ gabungan}} = \text{rata-rata nilai statistika kelas 9A}\)
Gunakan rumus rata-rata gabungan:
\(\color{blue} \bar {x}_{\text{ gabungan}} = \dfrac{\bar {x}_1 \cdot \text{n}_1 + \bar {x}_2 \cdot \text{n}_2 }{\text{n}_1 + \text{n}_2}\)
Jumlah siswa laki-laki 4 kurangnya dari jumlah siswa perempuan, artinya \(\text{n}_1 = \text{n}_2\:-\:4\)
Jumlah seluruh siswa di kelas 9A adalah 40 siswa,
\(\text{n}_1 + \text{n}_2 = 40\)
\(\text{n}_2\:-\:4 + \text{n}_2 = 40\)
\(2\text{n}_2 = 40 + 4\)
\(\text{n}_2 = \frac{44}{2} = 22\)
\(\text{n}_1 = 18\)
Banyaknya siswa perempuan ada 22 orang dan siswa laki-laki ada 18 orang
\(\bar {x}_{\text{ gabungan}} = \dfrac{85\cdot 18 + 90 \cdot 22}{18 + 22}\)
\(\bar {x}_{\text{ gabungan}} = \dfrac{1530 + 1980}{40}\)
\(\bar {x}_{\text{ gabungan}} = \dfrac{3510}{40}\)
\(\bar {x}_{\text{ gabungan}} = 87,75\)
-
Pertanyaan 16 dari 17
16. Pertanyaan
1 pointsSebuah kerucut memiliki luas selimut 550 cm² dan volume 1232 cm³. Jika panjang garis pelukis kerucut tersebut 25 cm, maka tinggi kerucut tersebut adalah …
Benar
\(\text{Luas selimut kerucut } = \pi r s\)
\(550 \text{ cm}^2 = \frac{22}{7}\cdot r \cdot 25 \text{ cm}\)
\(550 = \frac{550}{7}\cdot r \)
\(r = \cancel{550} \times \frac{7}{\cancel{550}}\)
\(r = 7 \text{ cm}\)
\(\text{Volume kerucut } = \frac{1}{3}\cdot \pi r^2 t\)
\(1232 \text{ cm}^3 = \frac{1}{3}\cdot \frac{22}{7}\cdot r^2 t\)
\(1232 = \frac{1}{3}\cdot \frac{22}{\cancel{7}}\cdot \cancel{7} \cdot 7 \cdot t\)
\(1232 = \frac{154}{3} t\)
\(t = \frac{3}{\cancel{154}}\times \cancelto{8}{1232}\)
\(t = 24 \text{ cm}\)
Jadi, tinggi kerucut tersebut adalah 24 cm
Salah
\(\text{Luas selimut kerucut } = \pi r s\)
\(550 \text{ cm}^2 = \frac{22}{7}\cdot r \cdot 25 \text{ cm}\)
\(550 = \frac{550}{7}\cdot r \)
\(r = \cancel{550} \times \frac{7}{\cancel{550}}\)
\(r = 7 \text{ cm}\)
\(\text{Volume kerucut } = \frac{1}{3}\cdot \pi r^2 t\)
\(1232 \text{ cm}^3 = \frac{1}{3}\cdot \frac{22}{7}\cdot r^2 t\)
\(1232 = \frac{1}{3}\cdot \frac{22}{\cancel{7}}\cdot \cancel{7} \cdot 7 \cdot t\)
\(1232 = \frac{154}{3} t\)
\(t = \frac{3}{\cancel{154}}\times \cancelto{8}{1232}\)
\(t = 24 \text{ cm}\)
Jadi, tinggi kerucut tersebut adalah 24 cm
-
Pertanyaan 17 dari 17
17. Pertanyaan
1 pointsJika \(\sqrt[4] {81 x^8} = 48\), maka nilai \(x\) yang memenuhi adalah …
Benar
\(\sqrt[4] {81 x^8} = 48\)
\(\sqrt[4] {3^4 x^8} = 48\)
\(3^{\frac{4}{4}} x^{\frac{8}{4}} = 48\)
\(3x^2 = 48\)
\(x^2 = 16\)
\(x = \pm \sqrt{16} = \pm 4\)
Salah
\(\sqrt[4] {81 x^8} = 48\)
\(\sqrt[4] {3^4 x^8} = 48\)
\(3^{\frac{4}{4}} x^{\frac{8}{4}} = 48\)
\(3x^2 = 48\)
\(x^2 = 16\)
\(x = \pm \sqrt{16} = \pm 4\)
