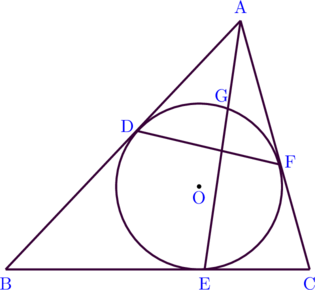
Terdapat lingkaran yang berpusat di titik O dan berada di dalam segitiga ABC. AB menyinggung lingkaran di titik D, AC menyinggung lingkaran di titik F, dan BC menyinggung lingkaran di titik E. AE memotong lingkaran di titik G. DF dan AE saling berpotongan. Besar sudut BAC = 60°, panjang AD = \(x\) cm, panjang BD = 4 cm, dan panjang FC = 2 cm.
Tentukan:
(1) \(\dfrac{\text{Luas } \triangle \text{ ADF}}{\text{AG} \times \text{AE}} = \dotso\)
(2) Panjang sisi BC
(3) Nilai \(x\)
(1) \(\dfrac{1}{4}\sqrt{3}\)
Perhatikan \(\triangle \text{DAF}\) sama kaki, AD = AF (garis singgung yang sama panjangnya)
Garis AD dan AE sama-sama ditarik dari titik A, memiliki hubungan \(\text{AD}^2 = \text{AG} \times \text{AE}\)
\(\dfrac{\text{Luas segitiga DAF}}{\text{AG} \cdot \text{AE}} = \dfrac{\dfrac{1}{2} \cdot \text{AD} \cdot \text{AF} \cdot \sin 60^{\circ}}{\text{AD}^2}\)
\(\dfrac{\text{Luas segitiga DAF}}{\text{AG} \cdot \text{AE}} = \dfrac{\dfrac{1}{2} \cdot \text{AD} \cdot \text{AD} \cdot \sin 60^{\circ}}{\text{AD}^2}\)
\(\dfrac{\text{Luas segitiga DAF}}{\text{AG} \cdot \text{AE}} = \dfrac{\dfrac{1}{2} \cdot \cancel{\text{AD}^2} \cdot \dfrac{1}{2} \sqrt{3}}{\cancel{\text{AD}^2}}\)
\(\dfrac{\text{Luas segitiga DAF}}{\text{AG} \cdot \text{AE}} = \dfrac{1}{4} \sqrt{3}\)
(2) 6 cm
Perhatikan bahwa BD = BE dan CF = CE
BC = BE + EC
BC = BD + FC
BC = 4 + 2
BC = 6 cm
(3) \((\sqrt{33}\:-\:3)\) cm
Perhatikan segitiga ABC, gunakan aturan cosinus.
Panjang AD = AF = \(x\) cm
\(\text{BC}^2 = \text{AB}^2 + \text{AC}^2 \:-\:2 \text{AB} \cdot \text{AC} \cdot \cos 60^{\circ}\)
\(6^2 = (x + 4)^2 + (x + 2)^2 \:-\:\cancel{2} \cdot (x + 4)(x + 2) \cdot \dfrac{1}{\cancel{2}}\)
\(36 = x^2 + 8x + 16 + x^2 + 4x + 4 \:-\:(x^2 + 6x + 8) \)
\(36 = x^2 + 8x + 16 + x^2 + 4x + 4 \:-\:x^2 \:-\:6x \:-\:8\)
\(36 = x^2 + 6x + 12\)
\(0 = x^2 + 6x \:-\:24\)
\(x = \dfrac{-b \pm \sqrt{b^2 \:-\:4ac}}{2a}\)
\(x = \dfrac{-6 \pm \sqrt{6^2 \:-\:4(1)(-24)}}{2(1)}\)
\(x = \dfrac{-6 \pm \sqrt{36 + 96}}{2}\)
\(x = \dfrac{-6 + \sqrt{132}}{2}\)
\(x = \dfrac{-6 + 2\sqrt{33}}{2}\)
\(x = -3 + \sqrt{33}\text{ cm}\)
\(x = (\sqrt{33}\:-\:3)\text{ cm}\)
